Question

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B.

（1）求证：△ADF∽△DEC

（2）若AB=4,AD=3,AE=3,求AF的长.

 

 

Answer 1

(1)证明见解析；（2）.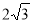

【解析】

试题分析：（1）利用对应两角相等，证明两个三角形相似△ADF∽△DEC；

（2）利用△ADF∽△DEC，可以求出线段DE的长度；然后在在Rt△ADE中，利用勾股定理求出线段AE的长度．

试题解析：（1）证明：∵四边形ABCD是平行四边形

∴AD∥BC AB∥CD

∴∠ADF=∠CED ∠B+∠C=180°

∵∠AFE+∠AFD=180 ∠AFE=∠B

∴∠AFD=∠C

∴△ADF∽△DEC

(2)【解析】
∵四边形ABCD是平行四边形

∴AD∥BC CD=AB=4

又∵AE⊥BC

∴ AE⊥AD

在Rt△ADE中，DE=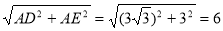

∵△ADF∽△DEC

∴

∴

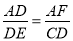
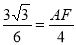
AF=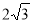

考点：1.相似三角形的判定与性质；2.勾股定理；3.平行四边形的性质．