
如图,在直角梯形ABCD中,AD//BC,?ABC=90?,BD ?DC,BD=DC,CE平分?BCD,交AB于点E,交BD于点H,EN//DC交BD于点N。下列结论:
①BH=DH;②CH=( 1)EH;③
1)EH;③ =
= ;
;
其中正确的是
A.①②③ B.只有②③ C.只有② D.只有③

B.
【解析】
试题分析:①如图,过H作HM⊥BC于M,
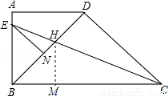
根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;
②设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用相似三角形的性质即可结论②;
③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.
故选B.
考点:直角梯形.


科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:解答题
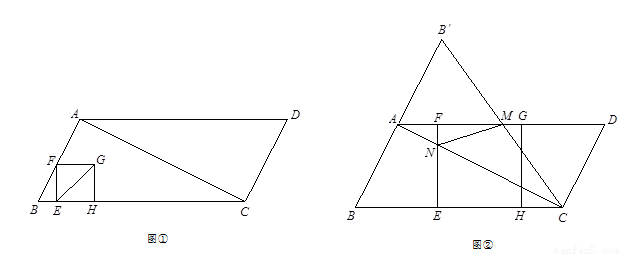
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)、你认为 和 组合,△ABC和△DEF不一定全等,
(2)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用①、②、③、④、⑤表示);
(3)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.


查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:填空题
如图,AB是⊙O的直径,若∠BAC=350,则∠ADC=__________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
沈阳地铁2号线的开通,方便了市民的出行.从2012年1月9日到2月7日的30天里,累计客运量约达3040000人次,将3040000用科学记数法表示为( )
A.3.04×105 B.3.04×106 C.30.4×105 D.0.304×107
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:解答题
为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:填空题
“节约光荣,浪费可耻”,据统计我国每年浪费粮食约8000000吨,这个数据用科学记数法可表示为 吨.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com