
【题目】如图,∠CDE+∠CED=90°,EM平分∠CED,并与CD边交于点M.DN平分∠CED,并与EM交于点N.
(1)依题意补全图形,并猜想∠EDN+∠NED的度数等于 ;
(2)证明以上结论.
证明:∵DN平分∠CDE,EM平分∠CED,
∴∠EDN=![]() ∠CDE,∠NED= .(理由: )
∠CDE,∠NED= .(理由: )
∵∠CDE+∠CED=90°,
∴∠EDN+∠NED= ×(∠ +∠ )= ×90°= °.
【答案】45°;![]() ∠CED;角平分线的定义;
∠CED;角平分线的定义;![]() ;CDE;CED;
;CDE;CED;![]() ;45
;45
【解析】(1)解:如图所示: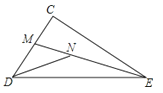
猜想∠EDN+∠NED=45°.
(2)证明:∵DN平分∠CDE,EM平分∠CED,
∴∠EDN=![]() ∠CDE,∠NED=
∠CDE,∠NED=![]() ∠CED.(理由:角平分线的定义),
∠CED.(理由:角平分线的定义),
∵∵∠CDE+∠CED=90°,
∴∠EDN+∠NED=![]() (∠CDE+∠CED)=
(∠CDE+∠CED)=![]() x900=45°.
x900=45°.
所以答案是:(1)45°;(2)![]() ∠CED;角平分线的定义;
∠CED;角平分线的定义;![]() ;CDE;CED;
;CDE;CED;![]() ;45.
;45.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
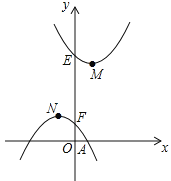
【题目】如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1
(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.
(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为______,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是______.
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年3月份,某市深陷“十面霾伏”,一周空气质量报告中某项污染指数是:231,235,231,234,230,231,225,则这组数据的中位数,众数分别是( )
A.232,231
B.231,232
C.231,231
D.232,235
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理判断题七年级五个班的班长因为参加校学生干部培训会而没有观看年级的乒乓球比赛.年级组长让他们每人猜一猜其中两个班的比赛名次.这五个班长各自猜测的结果如表所示: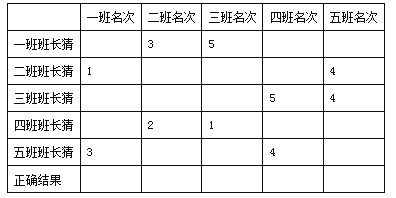
年级组长说,每班的名次都至少被他们中的一人说对了,请你根据以上信息将一班~五班的正确名次填写在表中最后一行.
查看答案和解析>>
科目:初中数学 来源: 题型:
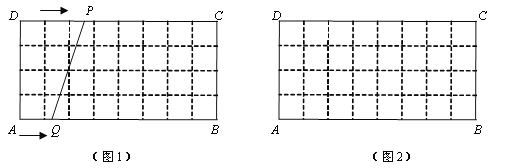
【题目】如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).
(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ并求其长度;
(2)当t为多少时,△PQB是以BP为底的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧的长度y(cm)是所挂物体质量X(kg)的一次函数.某弹簧不挂物体时,长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm.
(1)写出y与x之间的关系式;
(2)并求当所挂物体的质量为4kg时弹簧的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com