
【题目】在 Rt ![]() 中,
中,![]() ,
, ![]() ,点
,点 ![]() 为射线
为射线 ![]() 上一点,连接
上一点,连接 ![]() ,过点
,过点 ![]() 作线段
作线段 ![]() 的垂线
的垂线 ![]() ,在直线
,在直线 ![]() 上,分别在点
上,分别在点 ![]() 的两侧截取与线段
的两侧截取与线段 ![]() 相等的线段
相等的线段 ![]() 和
和 ![]() ,连接
,连接 ![]() ,
,![]() .
.
(1)当点 ![]() 在线段
在线段 ![]() 上时(点
上时(点 ![]() 不与点
不与点 ![]() ,
,![]() 重合),如图1,
重合),如图1,
①请你将图形补充完整;
②线段 ![]() ,
,![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段 ![]() ,
,![]() 的数量关系为 ;
的数量关系为 ;

(2)当点 ![]() 在线段
在线段 ![]() 的延长线上时,如图2,
的延长线上时,如图2,
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

【答案】(1)①见详解,②垂直、相等;(2)①见详解,②成立,理由见详解
【解析】
(1)①D在线段AB上时,在直线l上截取CE=CF=CD,即可画出图象.②在图1中证明△ACD≌△BCF得到AD=BF,∠BAC=∠FBC,利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
(2)①D在线段AB延长线上时,在直线l上截取CE=CF=CD,即可画出图象.②在图2中证明△ACD≌△BCF得到AD=BF,∠BAC=∠FBC,利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
解:(1)①见图1所示.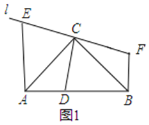
②证明:∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠ACB=∠DCF,
∴∠ACD=∠BCF
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
故答案为:垂直、相等.
(2)①见图2所示.
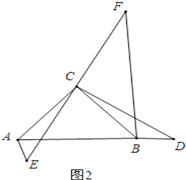
②成立.理由如下:
证明:∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠DCF+∠BCD=∠ACB+∠BCD,
即∠ACD=∠BCF,
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.
(1)求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;
(2)该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
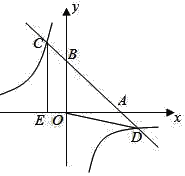
【题目】如图,直角坐标系xOy中,直线y=﹣x+b分别交x,y轴的正半轴于点A,B,交反比例函数y=﹣![]() 的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() ,则CD的长为____.
,则CD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列六个命题:①相等的角是对顶角;②两直线平行,同位角相等;③若一个三角形的两个内角分别为![]() 和
和![]() ,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
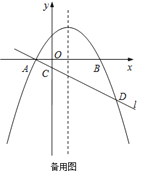
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() ,
,![]() 用含
用含![]() 的式子表示);
的式子表示);
![]() 点
点![]() 是直线
是直线![]() 上方的抛物线上的一点,若
上方的抛物线上的一点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
![]() 设
设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
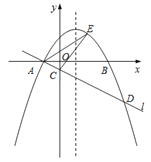
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,DE⊥AB于点E,DF⊥AC于点F,BD=CD
求证:DE=DF

证明:∵AB=AC
∴∠B=∠C( ),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF( ).
∴DE=DF( )
(1)请在括号里写出推理的依据.
(2)请你写出另一种证明此题的方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com