
【题目】如图,在△ABC,AB=AC,DE⊥AB于点E,DF⊥AC于点F,BD=CD
求证:DE=DF

证明:∵AB=AC
∴∠B=∠C( ),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF( ).
∴DE=DF( )
(1)请在括号里写出推理的依据.
(2)请你写出另一种证明此题的方法.
【答案】(1)等边对等角;AAS;全等三角形的对应边相等;(2)见解析
【解析】
(1)由AB=AC得∠B=∠C是依据“等边对等角”,由判定条件可知全等的依据是“AAS”,由全等得对应边相等是依据全等三角形的性质,据此作答即可;
(2)连接AD,根据等腰三角形三线合一的性质和角平分线的性质定理即可得证;
解:(1)证明:∵AB=AC
∴∠B=∠C(等边对等角),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF(AAS).
∴DE=DF(全等三角形的对应边相等)
故答案为等边对等角;AAS;全等三角形的对应边相等.
(2)连接AD.

∵AB=AC,BD=CD,
∴AD平分∠BAC,
又∵DE⊥AB,DF⊥AC,
∴DE=DF.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】在 Rt ![]() 中,
中,![]() ,
, ![]() ,点
,点 ![]() 为射线
为射线 ![]() 上一点,连接
上一点,连接 ![]() ,过点
,过点 ![]() 作线段
作线段 ![]() 的垂线
的垂线 ![]() ,在直线
,在直线 ![]() 上,分别在点
上,分别在点 ![]() 的两侧截取与线段
的两侧截取与线段 ![]() 相等的线段
相等的线段 ![]() 和
和 ![]() ,连接
,连接 ![]() ,
,![]() .
.
(1)当点 ![]() 在线段
在线段 ![]() 上时(点
上时(点 ![]() 不与点
不与点 ![]() ,
,![]() 重合),如图1,
重合),如图1,
①请你将图形补充完整;
②线段 ![]() ,
,![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段 ![]() ,
,![]() 的数量关系为 ;
的数量关系为 ;

(2)当点 ![]() 在线段
在线段 ![]() 的延长线上时,如图2,
的延长线上时,如图2,
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
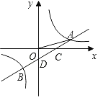
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 求一次函数的解析式;
求一次函数的解析式;
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 与
与![]() 相似,请你求出
相似,请你求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,
∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.

(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com