
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)证明见解析;(2)△AOD是直角三角形;(3)当α的度数为125 °或110 °或140 °时,△AOD是等腰三角形;
【解析】
(1)首先由旋转的定义和性质得到CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;(2)根据旋转前后对应的两个三角形全等可得△BOC≌△ADC,利用全等三角形的性质得到∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,据此判断△AOD的形状;(3)需要分三种情况讨论,即①要使AO=AD,需∠AOD=∠ADO;②要使OA=OD,需∠OAD=∠ADO;③要使OD=AD,需∠OAD=∠AOD,再分别建立关于α的方程,求出α的度数;
解:
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)当∠α=150°时,△AOD是直角三角形.理由如下:
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC-∠ODC=90°,
∴△AOD是直角三角形;
(3)①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
∵∠AOD=190°-α,∠OAD=![]() =120°-
=120°-![]() ,
,
∴190°-α=120°-![]() ,
,
解得α=140°.
综上所述:当α的度数为125 °或110 °或140 °时,△AOD是等腰三角形.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,DE⊥AB于点E,DF⊥AC于点F,BD=CD
求证:DE=DF

证明:∵AB=AC
∴∠B=∠C( ),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF( ).
∴DE=DF( )
(1)请在括号里写出推理的依据.
(2)请你写出另一种证明此题的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
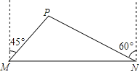
【题目】我市准备在相距![]() 千米的
千米的![]() ,
,![]() 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在![]() 地北偏东
地北偏东![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 处,有一个半径为
处,有一个半径为![]() 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.

(1)用直尺和圆规作射线![]() 平分
平分![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:角平分线上的点到角两边的距离相等. (要求:在第(1)小题作图的基础上,画出证明所需的图形,写出已知、求证和证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.

(1)请用两种不同方法,求②中阴影部分的面积(不用化简)
方法1: ;方法2: ;
(2)观察图②,写出(m+n)2,(m﹣n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com