
【题目】我市准备在相距![]() 千米的
千米的![]() ,
,![]() 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在![]() 地北偏东
地北偏东![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 处,有一个半径为
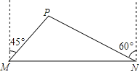
处,有一个半径为![]() 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ,
,![]() )
)
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
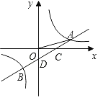
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 求一次函数的解析式;
求一次函数的解析式;
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 与
与![]() 相似,请你求出
相似,请你求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型建立:如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)模型应用:
①已知直线l1:![]() 与y轴交于
与y轴交于![]() 点,将直线l1绕着
点,将直线l1绕着![]() 点顺时针旋转45°至l2,如图2,求l2的函数解析式;
点顺时针旋转45°至l2,如图2,求l2的函数解析式;
②如图3,长方形ABCO,![]() 为坐标原点,
为坐标原点,![]() 的坐标为(8,6),
的坐标为(8,6),![]() 、
、![]() 分别在坐标轴上,
分别在坐标轴上,![]() 是线段
是线段![]() 上动点,点
上动点,点![]() 是直线
是直线![]() 上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点
上的一点,若△APD是以点D为直角顶点的等腰Rt△,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=![]() x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
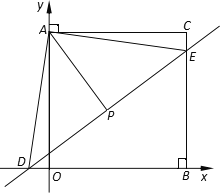
⑴ 求点D与点E的坐标; ⑵求证:△ADO≌△AEC;⑶ 求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com