
【题目】如图, 平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=![]() x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
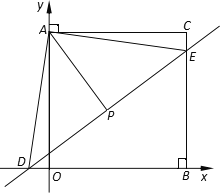
⑴ 求点D与点E的坐标; ⑵求证:△ADO≌△AEC;⑶ 求AP的长.
【答案】⑴点D(-4,0);点E(28,24);⑵ 见解析.⑶AP=20.
【解析】
(1)根据题意可求出E点横坐标为28,然后根据一次函数解析式即可求出D、E两点坐标;
(2)根据坐标即可求出OD=CE,然后根据题意即可证出四边形AOBC是正方形,从而得出AO =AC,∠AOD=∠C=90°,再利用SAS即可证出△ADO≌△AEC;
(3)根据全等三角形的性质可得:∠OAD=∠CAE,AD=AE,从而证出△ADE为等腰直角三角形,即可得到AP=![]() DE,然后利用勾股定理即可求出DE,从而求出AP.
DE,然后利用勾股定理即可求出DE,从而求出AP.
解:(1)∵CE垂直x轴,点C(28,28)
∴E点横坐标为28
∵一次函数y=![]() x+3的图像分别与x轴和CB交于点D、E
x+3的图像分别与x轴和CB交于点D、E
当y=0时,解得:x=-4,当x=28时,解得:y=24
∴点D的坐标为(-4,0),点E的坐标为(28,24)
(2)∵点D的坐标为(-4,0),点E的坐标为(28,24),点C(28,28)
∴OD=4,CE=28-24=4
∴OD=CE
∵过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,
∴四边形AOBC是正方形
∴AO =AC,∠AOD=∠C=90°,点B的坐标为(28,0)
在△ADO和△AEC中
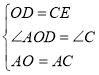
∴△ADO≌△AEC
(3)∵△ADO≌△AEC
∴∠OAD=∠CAE,AD=AE
∴∠OAD+∠OAE=∠CAE+∠OAE
∴∠DAE=∠OAC=90°
∴△ADE为等腰直角三角形
∵点P 是DE中点
∴AP=![]() DE
DE
∵点B的坐标为(28,0),点D(-4,0),点E(28,24)
∴BD=28-(-4)=32,BE=24-0=24
根据勾股定理:DE=![]()
∴AP=![]() DE=20
DE=20


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】我市准备在相距![]() 千米的
千米的![]() ,
,![]() 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在![]() 地北偏东
地北偏东![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 处,有一个半径为
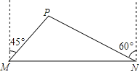
处,有一个半径为![]() 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.

(1)请用两种不同方法,求②中阴影部分的面积(不用化简)
方法1: ;方法2: ;
(2)观察图②,写出(m+n)2,(m﹣n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系XOY中,一次函数y=kx-k的图象经过A(2,2),与x轴、y轴分别交于点C、点B.
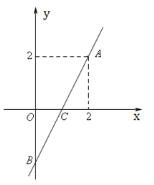
(1)观察图像,直接写出使y≥0的x的取值范围;
(2)求一次函数的解析式;
(3)若点P是x轴上一点,且满足△PAB的面积是6,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的网格中,△ABC的顶点A的坐标为(1,1)
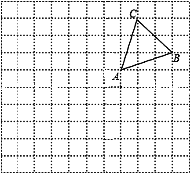
⑴建立平面直角坐标系,画出△ABC关于y轴对称的△A1B1C1;并分别写出点B1的坐标是 、点C1的坐标是
⑵①借助图中的网格,请只用直尺(无刻度)在图中找一点P,使得P到AB、AC的距离相等,且使PA=PB.
②若动点Q在y轴上,使得△QAC的周长最小,则△QAC的最小周长= .(友情提醒:别忘标注宇母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,按如下步骤作图:
,按如下步骤作图:
①分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径在
的长为半径在![]() 两边作弧,交于两点
两边作弧,交于两点![]() 、
、![]() ;
;
②作直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
③过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
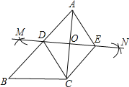
![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 当
当![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com