
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.

(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=![]() x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
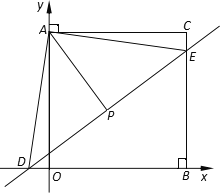
⑴ 求点D与点E的坐标; ⑵求证:△ADO≌△AEC;⑶ 求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,无论k取何实数,直线y=(k-1)x+4-5k总经过定点P,则点P与动点Q(5m-1,5m+1)的距离的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲.乙两种商品原来的单价分别为x元.y元,则可列方程组为_________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
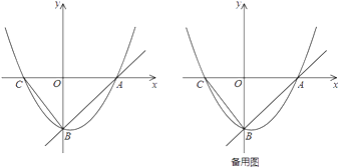
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点 ![]() 在抛物线上,连接
在抛物线上,连接 ![]() ,当
,当 ![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,
运动, ![]() 、
、![]() 的运动速度都是每秒
的运动速度都是每秒![]() 个单位长度,当
个单位长度,当![]() 点到达
点到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动,试问在坐标平面内是否存在点
同时停止运动,试问在坐标平面内是否存在点![]() ,使
,使![]() 、
、![]() 运动过程中的某一时刻,以
运动过程中的某一时刻,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形?若存在,直接写出点
为顶点的四边形为菱形?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
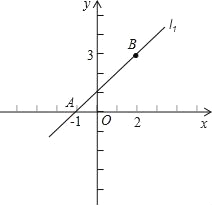
【题目】如图,已知直线l1:y=kx+1,与x轴相交于点A,同时经过点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).
(1)求l1的解析式;
(2)若S△APB=3,求P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com