
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
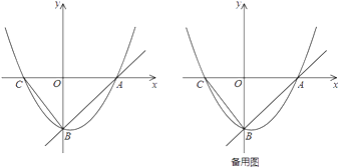
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点 ![]() 在抛物线上,连接
在抛物线上,连接 ![]() ,当
,当 ![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,
运动, ![]() 、
、![]() 的运动速度都是每秒
的运动速度都是每秒![]() 个单位长度,当
个单位长度,当![]() 点到达
点到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动,试问在坐标平面内是否存在点
同时停止运动,试问在坐标平面内是否存在点![]() ,使
,使![]() 、
、![]() 运动过程中的某一时刻,以
运动过程中的某一时刻,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形?若存在,直接写出点
为顶点的四边形为菱形?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() ,
,![]() 或
或![]() (3)
(3)![]() 或
或![]() 或
或![]()
【解析】
(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式,进而求出点C的坐标;
(2)满足条件的点M有两种情形,需要分类讨论:
①当BM⊥BC时,如答图2-1所示;
②当BM与BC关于y轴对称时,如答图2-2所示.
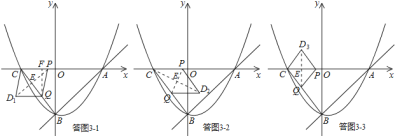
(3)△CPQ的三边均可能成为菱形的对角线,以此为基础进行分类讨论:
①若以CQ为菱形对角线,如答图3-1.此时BQ=t,菱形边长=t;
②若以PQ为菱形对角线,如答图3-2.此时BQ=t,菱形边长=t;
③若以CP为菱形对角线,如答图3-3.此时BQ=t,菱形边长=5-t.
解:![]() 直线解析式
直线解析式![]() ,
,
令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() .
.
∴![]() 、
、![]() .
.
∵点![]() 、
、![]() 在抛物线
在抛物线![]() 上,
上,
∴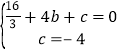 ,
,
解得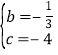 ,
,
∴抛物线解析式为:![]() .
.
令![]() ,
,
解得:![]() 或
或![]() ,
,
∴![]() .
.![]() ,
,
设![]() ,
,
①当![]() 时,如答图
时,如答图![]() 所示.
所示.
∵![]() ,
,
∴![]() ,故点
,故点![]() 满足条件.
满足条件.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.
联立![]() 与
与![]() ,
,
得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
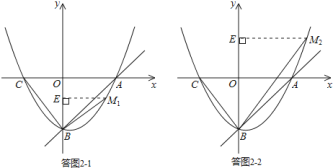
②当![]() 与
与![]() 关于
关于![]() 轴对称时,如答图
轴对称时,如答图![]() 所示.
所示.
∵![]() ,
,![]() ,
,
∴![]() ,
,
故点![]() 满足条件.
满足条件.
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
则![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.
联立![]() 与
与![]() 得:
得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
综上所述,满足条件的点![]() 的坐标为:
的坐标为:![]() 或
或![]() .
.
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
假设存在满足条件的点![]() ,设菱形的对角线交于点
,设菱形的对角线交于点![]() ,设运动时间为
,设运动时间为![]() .
.
①若以![]() 为菱形对角线,如答图
为菱形对角线,如答图![]() .此时
.此时![]() ,菱形边长
,菱形边长![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
解得![]() .
.
∴![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
则![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 与点
与点![]() 横坐标相差
横坐标相差![]() 个单位,
个单位,
∴![]() ;
;
②若以![]() 为菱形对角线,如答图
为菱形对角线,如答图![]() .此时
.此时![]() ,菱形边长
,菱形边长![]() .
.
∵![]() ,
,
∴![]() ,点
,点![]() 为
为![]() 中点,
中点,
∴![]() .
.
∵点![]() 与点
与点![]() 横坐标相差
横坐标相差![]() 个单位,
个单位,
∴![]() ;
;
③若以![]() 为菱形对角线,如答图
为菱形对角线,如答图![]() .此时
.此时![]() ,菱形边长
,菱形边长![]() .
.
在![]() 中,
中,![]() ,
,
解得![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
综上所述,存在满足条件的点![]() ,点
,点![]() 坐标为:
坐标为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.

(1)用直尺和圆规作射线![]() 平分
平分![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:角平分线上的点到角两边的距离相等. (要求:在第(1)小题作图的基础上,画出证明所需的图形,写出已知、求证和证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的网格中,△ABC的顶点A的坐标为(1,1)
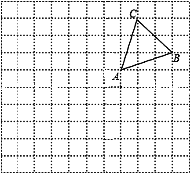
⑴建立平面直角坐标系,画出△ABC关于y轴对称的△A1B1C1;并分别写出点B1的坐标是 、点C1的坐标是
⑵①借助图中的网格,请只用直尺(无刻度)在图中找一点P,使得P到AB、AC的距离相等,且使PA=PB.
②若动点Q在y轴上,使得△QAC的周长最小,则△QAC的最小周长= .(友情提醒:别忘标注宇母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD和△BCE中, AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
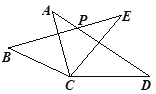
A.110°B.125°C.130°D.155°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A的纵坐标为2, 动点P沿路线![]() 运动.
运动.
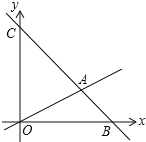
(1)求直线BC的解析式;
(2)在y轴上找一点M,使得△MAB的周长最小,则点M的坐标为______;(请直接写出结果)
(3)当△OPC的面积是△OAC的面积的![]() 时,求出这时P的坐标.
时,求出这时P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
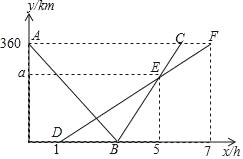
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com