
【题目】如图,已知![]() .
.

(1)用直尺和圆规作射线![]() 平分
平分![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:角平分线上的点到角两边的距离相等. (要求:在第(1)小题作图的基础上,画出证明所需的图形,写出已知、求证和证明过程)
【答案】(1)见解析;(2)见解析.
【解析】
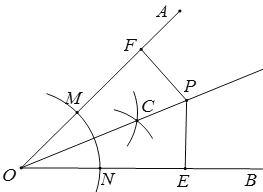
(1)以点O为圆心,以任意长为半径画弧,与OA、OB分别交于点M、N,然后分别以点M、N为圆心,以大于![]() MN长为半径画弧,两弧交于点C,作射线OC即可;
MN长为半径画弧,两弧交于点C,作射线OC即可;
(2)在OC上任意取一点P,然后画出符合题意的图形,利用AAS证明△POE≌△POF,再根据全等三角形的对应边得到PE=PF即可.
(1)如图,射线OC即为所求作的;

(2)如图,OC平分∠AOB,P为OC上任意一点,PE⊥OB,PF⊥OA,垂足分别为E、F,求证:PE=PF.
证明:∵OC平分∠AOB,
∴∠AOP=∠BOP,
又∵PE⊥OB,PF⊥OA,
∴∠PEO=∠PFO=90°,
在△POE和△POF中,
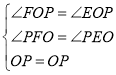 ,
,
∴△POE≌△POF(AAS),
∴PE=PF,
即角平分线上的点到角两边的距离相等.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
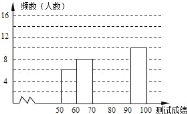
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)①频数分布表中a的值为;②若测试成绩不低于80分为优秀,则本次测试的优秀率是;③将频数分布直方图补充完整;
(2)第5组10名同学中,有4名男同学(用A,B,C,D表示),现将这4名同学分成两组(每组2人)进行对抗练习,求A与B两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.

(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
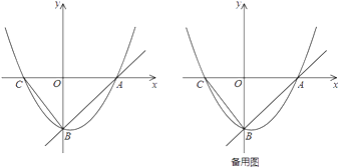
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点 ![]() 在抛物线上,连接
在抛物线上,连接 ![]() ,当
,当 ![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 由
由![]() 向
向![]() 运动,
运动, ![]() 、
、![]() 的运动速度都是每秒
的运动速度都是每秒![]() 个单位长度,当
个单位长度,当![]() 点到达
点到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动,试问在坐标平面内是否存在点
同时停止运动,试问在坐标平面内是否存在点![]() ,使
,使![]() 、
、![]() 运动过程中的某一时刻,以
运动过程中的某一时刻,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形?若存在,直接写出点
为顶点的四边形为菱形?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com