
【题目】直线![]() 与直线
与直线![]() ,它们在同一个坐标系中的图像大致( ).
,它们在同一个坐标系中的图像大致( ).
A.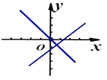 B.
B.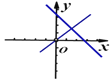
C.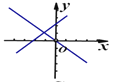 D.
D.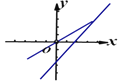
【答案】A
【解析】
根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得kb的符号,从而判断y=kbx的图象是否正确,进而比较可得答案.
根据一次函数的图象分析可得:
A.由一次函数y=kx+b图象可知k>0,b<0,即kb<0,由一次函数y=kbx的图象可知kb<0,两函数解析式均成立;
B.由一次函数y=kx+b图象可知k<0,b>0,即kb<0,由一次函数y=kbx的图象可知kb>0,矛盾;
C.由一次函数y=kx+b图象可知k>0,b>0,即kb>0,由一次函数y=kbx的图象可知kb<0,矛盾;
D.由一次函数y=kx+b图象可知k>0,b<0,即kb<0,由一次函数y=kbx的图象可知kb>0,矛盾.
故选A.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
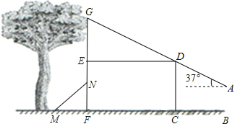
【题目】身高![]() 米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形
米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形![]() 代表建筑物,兵兵位于建筑物前点
代表建筑物,兵兵位于建筑物前点![]() 处,风筝挂在建筑物上方的树枝点
处,风筝挂在建筑物上方的树枝点![]() 处(点
处(点![]() 在
在![]() 的延长线上).经测量,兵兵与建筑物的距离
的延长线上).经测量,兵兵与建筑物的距离![]() 米,建筑物底部宽
米,建筑物底部宽![]() 米,风筝所在点
米,风筝所在点![]() 与建筑物顶点
与建筑物顶点![]() 及风筝线在手中的点
及风筝线在手中的点![]() 在同一条直线上,点
在同一条直线上,点![]() 距地面的高度
距地面的高度![]() 米,风筝线与水平线夹角为
米,风筝线与水平线夹角为![]() .
.
![]() 求风筝距地面的高度
求风筝距地面的高度![]() ;
;
![]() 在建筑物后面有长
在建筑物后面有长![]() 米的梯子
米的梯子![]() ,梯脚
,梯脚![]() 在距墙
在距墙![]() 米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根
米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根![]() 米长的竹竿能否触到挂在树上的风筝?
米长的竹竿能否触到挂在树上的风筝?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
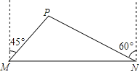
【题目】我市准备在相距![]() 千米的
千米的![]() ,
,![]() 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在![]() 地北偏东
地北偏东![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 处,有一个半径为
处,有一个半径为![]() 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.

(1)用直尺和圆规作射线![]() 平分
平分![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:角平分线上的点到角两边的距离相等. (要求:在第(1)小题作图的基础上,画出证明所需的图形,写出已知、求证和证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条![]() ,其中
,其中![]() ,
,![]() .然后在纸条上任意画一条截线段
.然后在纸条上任意画一条截线段![]() ,将纸片沿
,将纸片沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() .如图2所示:
.如图2所示:

探究:
(1)若![]() ,
,![]() ______°;
______°;
(2)改变折痕![]() 位置,
位置,![]() 始终是______三角形,请说明理由;
始终是______三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究![]() 的面积时,发现
的面积时,发现![]() 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出![]() 的面积最小值为
的面积最小值为![]() ,此时
,此时![]() 的大小可以为______°;
的大小可以为______°;
(4)小明继续动手操作,发现了![]() 面积的最大值.请你求出这个最大值.
面积的最大值.请你求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.

(1)请用两种不同方法,求②中阴影部分的面积(不用化简)
方法1: ;方法2: ;
(2)观察图②,写出(m+n)2,(m﹣n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系XOY中,一次函数y=kx-k的图象经过A(2,2),与x轴、y轴分别交于点C、点B.
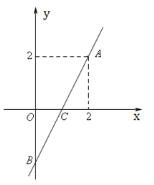
(1)观察图像,直接写出使y≥0的x的取值范围;
(2)求一次函数的解析式;
(3)若点P是x轴上一点,且满足△PAB的面积是6,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com