
ЁОЬтФПЁПЭМЂйЪЧвЛИіГЄЮЊ2mЃЌПэЮЊ2nЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљдШЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓАДЭМЂкаЮзДЦДГЩвЛИіе§ЗНаЮЃЎ

ЃЈ1ЃЉЧыгУСНжжВЛЭЌЗНЗЈЃЌЧѓЂкжавѕгАВПЗжЕФУцЛ§ЃЈВЛгУЛЏМђЃЉ
ЗНЗЈ1ЃКЁЁ ЁЁЃЛЗНЗЈ2ЃКЁЁ ЁЁЃЛ
ЃЈ2ЃЉЙлВьЭМЂкЃЌаДГіЃЈm+nЃЉ2ЃЌЃЈmЉnЃЉ2ЃЌmnжЎМфЕФЕШСПЙиЯЕ ЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЬтжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃК
ЂйШєa+bЃН7ЃЌabЃН5ЃЌЧѓЃЈaЉbЃЉ2ЕФжЕЃЛ
ЂкШє2a+bЃН5ЃЌabЃН2ЃЌЧѓ2aЉbЕФжЕЃЎ
ЁОД№АИЁП(1) ЃЈm+nЃЉ2Љ4mmЃЌЃЈmЉnЃЉ2ЃЛ(2) m2+2mn+n2Љ4mnЃНm2Љ2mn+n2ЃНЃЈmЉnЃЉ2;(3) Ђй29; ЂкЁР3
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвбжЊЭМаЮНсКЯБпГЄЮЊЃЈm+nЃЉЕФДѓе§ЗНаЮЕФУцЛ§МѕШЅГЄЮЊmЃЌПэЮЊnЕФ4ИіГЄЗНаЮУцЛ§вдМАБпГЄЮЊЃЈm-nЃЉЕФе§ЗНаЮЕФУцЛ§ЃЌЗжБ№ЧѓГіД№АИЃЛ
ЃЈ2ЃЉЗжБ№ЛЏМђЃЈ1ЃЉжаЧѓЕУвѕгАВПЗжЕФУцЛ§ПЩЕУД№АИЃЛ
ЃЈ3ЃЉЂйЂкРћгУЃЈ2ЃЉжаЙиЯЕЪНЃЌНЋвбжЊБфаЮЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉЗНЗЈ1ЃКЃЈm+nЃЉ2Љ4mnЃЌ
ЗНЗЈ2ЃКЃЈmЉnЃЉ2ЃЛ
ЙЪД№АИЮЊЃКЃЈm+nЃЉ2Љ4mnЃЛЃЈmЉnЃЉ2ЃЛ
ЃЈ2ЃЉЃЈm+nЃЉ2Љ4mnЃНЃЈmЉnЃЉ2
жЄУїЃКзѓБпЃНm2+2mn+n2Љ4mn
ЃНm2Љ2mn+n2
ЃНЃЈmЉnЃЉ2ЃНгвБпЃЛ
ЃЈ3ЃЉЂйЃЈaЉbЃЉ2ЃНЃЈa+bЃЉ2Љ4ab
ЃН72Љ4ЁС5
ЃН49Љ20=29ЃЛ
ЂкЃЈ2aЉbЃЉ2ЃНЃЈ2a+bЃЉ2Љ8ab
ЃН52Љ8ЁС2
ЃН25Љ16=9ЃЛ
Ёр2aЉbЃНЁР3ЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
![]() ЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
![]() ЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
![]() дк
дк![]() жсЩЯДцдквЛЕу
жсЩЯДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ЯрЫЦЃЌЧыФуЧѓГі
ЯрЫЦЃЌЧыФуЧѓГі![]() ЕуЕФзјБъЃЎ
ЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOЪЧЕШБпЁїABCФквЛЕуЃЎНЋЁїBOCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ60ЁуЕУЁїADCЃЌСЌНгODЃЎвбжЊЁЯAOB=110ЁуЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїCODЪЧЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉЕБІС=150ЁуЪБЃЌЪдХаЖЯЁїAODЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЬНОПЃКЕБІСЮЊЖрЩйЖШЪБЃЌЁїAODЪЧЕШбќШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯп![]() гыжБЯп
гыжБЯп![]() ЃЌЫќУЧдкЭЌвЛИізјБъЯЕжаЕФЭМЯёДѓжТЃЈ ЃЉЃЎ
ЃЌЫќУЧдкЭЌвЛИізјБъЯЕжаЕФЭМЯёДѓжТЃЈ ЃЉЃЎ
A.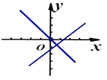 B.
B.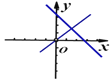
C.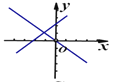 D.
D.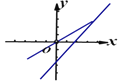
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
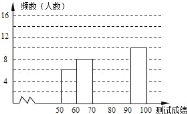
ЁОЬтФПЁПЁАЩЭжаЛЊЪЋДЪЃЌбАЮФЛЏЛљвђЃЌЦЗЩњЛюжЎУРЁБЃЌФГаЃОйАьСЫЪзНьЁАжаЙњЪЋДЪДѓЛсЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБФЌаД50ЪзЙХЪЋДЪЃЌШєУПе§ШЗФЌаДГівЛЪзЙХЪЋДЪЕУ2ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
ЃЈ1ЃЉЂйЦЕЪ§ЗжВМБэжаaЕФжЕЮЊЃЛЂкШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЃЛЂлНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЕк5зщ10УћЭЌбЇжаЃЌга4УћФаЭЌбЇЃЈгУAЃЌBЃЌCЃЌDБэЪОЃЉЃЌЯжНЋет4УћЭЌбЇЗжГЩСНзщЃЈУПзщ2ШЫЃЉНјааЖдПЙСЗЯАЃЌЧѓAгыBСНУћФаЭЌбЇФмЗждкЭЌвЛзщЕФИХТЪЃЎ
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 50ЁмxЃМ60 | 6 |
Ек2зщ | 60ЁмxЃМ70 | 8 |
Ек3зщ | 70ЁмxЃМ80 | 14 |
Ек4зщ | 80ЁмxЃМ90 | a |
Ек5зщ | 90ЁмxЃМ100 | 10 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯACB=ЁЯECD=90ЁуЃЌAC=BCЃЌEC=DCЃЌЕуDдкABБпЩЯЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїACEЁеЁїBCDЃЎ
ЃЈ2ЃЉШєAE=3ЃЌAD=2ЃЎЧѓEDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЃЌЁЯC=90ЁуЃЌACЃМBCЃЌШєDЮЊBCЩЯвЛЕуЃЌЧвЕНAЃЌBСНЕуОрРыЯрЕШЃЎ

ЃЈ1ЃЉРћгУГпЙцЃЌзїГіЕуDЕФЮЛжУЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЃЈ2ЃЉСЌНсADЃЌШєAB=5ЃЌAC=3ЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
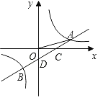
ЁОЬтФПЁПШчЭМ, ЦНУцжБНЧзјБъЯЕжаЃЌЙ§ЕуCЃЈ28ЃЌ28ЃЉЗжБ№зїxжсЁЂyжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊBЁЂAЃЌвЛДЮКЏЪ§y=![]() x+3ЕФЭМЯёЗжБ№гыxжсКЭCBНЛгкЕуDЁЂEЃЌЕуP ЪЧDEжаЕуЃЌСЌНгAP.
x+3ЕФЭМЯёЗжБ№гыxжсКЭCBНЛгкЕуDЁЂEЃЌЕуP ЪЧDEжаЕуЃЌСЌНгAP.
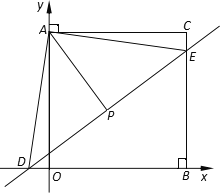
ЂХ ЧѓЕуDгыЕуEЕФзјБъЃЛ ЂЦЧѓжЄЃКЁїADOЁеЁїAECЃЛЂЧ ЧѓAPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
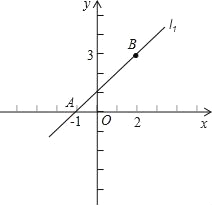
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпl1ЃКy=kx+1ЃЌгыxжсЯрНЛгкЕуAЃЌЭЌЪБОЙ§ЕуBЃЈ2ЃЌ3ЃЉЃЌСэвЛЬѕжБЯпl2ОЙ§ЕуBЃЌЧвгыxжсЯрНЛгкЕуPЃЈmЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓl1ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєSЁїAPB=3ЃЌЧѓPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com