
【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)根据∠ACB=∠ECD=90°求出∠DCB=∠ECA,根据SAS推出两三角形全等即可;
(2)根据等腰直角三角形求出∠BAC=∠B=45°,根据全等三角形的性质求出∠EAC=∠B=45°,求出∠EAD=90°,根据勾股定理求出即可.
【解答】(1)证明:∵∠ACB=∠ECD=90°,
∴∠ACB﹣∠ACD=∠ECD﹣∠ACD,
∴∠DCB=∠ECA,
在△ACE和△BCD中

∴△ACE≌△BCD(SAS);
(2)解:∵∠ACB=90°,AC=BC,
∴∠BAC=∠B=45°,
∵△ACE≌△BCD,
∴∠EAC=∠B=45°,
∴∠EAD=90°,
∴在Rt△AED中,∠EAD=90°,AE=3,AD=2,由勾股定理得:ED=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】“端午节”是中华民族古老的传统节日.甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案.
甲超市方案:购买该种粽子超过200元后,超出200元的部分按95%收费;
乙超市方案:购买该种粽子超过300元后,超出300元的部分按90%收费.
设某位顾客购买了x元的该种粽子.
(1)补充表格,填写在“横线”上:
(2)列式计算说明,如果顾客在“端午节”当天购买该种粽子超过200元,那么到哪家超市花费更少?
x (单位:元) | 实际在甲超市的花费 (单位:元) | 实际在乙超市的花费 (单位:元) |
0<x≤200 | x | x |
200<x≤300 | x | |
x>300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.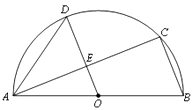
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯 | 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤280 | b |
三档 | x>280 | 0.82 |
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).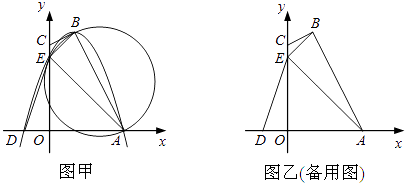
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列应用题:
⑴某房间的面积为17.6m2,房间地面恰好由110块相同的正方形地砖铺成,每块地砖的边长是多少?
⑵已知第一个正方体水箱的棱长是60cm,第二个正方体水箱的体积比第一个水箱的体积的3倍还多81000 cm3,则第二个水箱需要铁皮多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.

据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生,m的值是 .
(2)请根据据以上信息直在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com