
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


【答案】(1)见解析;(2)当D运动到BC中点时,AC⊥DE,理由见解析;(3)∠ADB=20°或40°或100°
【解析】
(1)根据SAS即可证明;
(2)当点D运动到BC中点时,AC⊥DE,由AB=AC知∠1=∠2,结合∠1=∠3,得出∠2=∠3.根据AE=AD,即可得;
(3)分三种情形分别求解即可解决问题;
解:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴△BAD ≌△CAE(SAS).
(2)当D运动到BC中点时,AC⊥DE .

∵D是BC中点,AB=AC ,∴∠1=∠2.
∵△BAD ≌△CAE,∴∠1=∠3.∴∠2=∠3.
∵AD=AE,∴AC⊥DE.
∴当D运动到BC中点时,AC⊥DE.
(3)∠ADB=20°或40°或100° .
理由:①如图,当点D在CB的延长线上时,
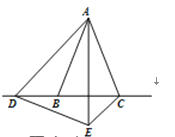
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC,
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,
∴△ABC是等边三角形,∴∠ABC=60°
∵△ABD中的最小角是∠BAD=20°,则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ABD=180°-20°-60°=100°.
③ 当点D在BC 延长线上时,最小角只能是∠ADB=20°,
综上所述,满足条件的∠ABD的值为20°或40°或100°.


科目:初中数学 来源: 题型:
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造![]() 个新公共自行车站点和配置
个新公共自行车站点和配置![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的5×8方格中,△ABC的顶点都在格点上.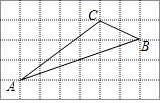
(1)在给定的方格中,以直线AB为对称轴,画出△ABC的轴对称图形△ABD.
(2)求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题: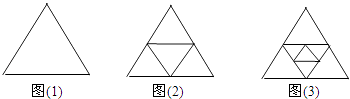
在第n个图形中有个三角形(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
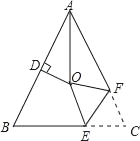
【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,玛丽在荡绳索过程中离地面的最低点的高度MN=_____.
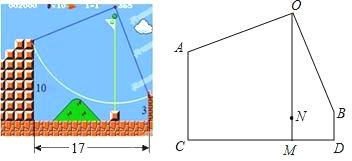
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(3ab-4)(3ab+4);
(2)(![]() π+
π+![]() )(
)(![]() π-
π-![]() );
);
(3)(-0.3x+0.2y)(-0.3x-0.2y);
(4)(![]() x-
x-![]() y)(-
y)(-![]() x-
x-![]() y).
y).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com