
【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题: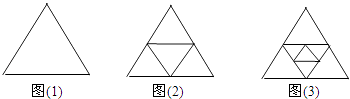
在第n个图形中有个三角形(用含n的式子表示).
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;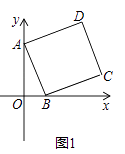
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )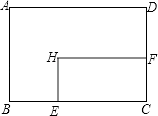
A.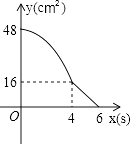
B.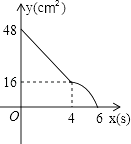
C.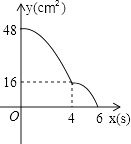
D.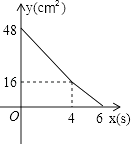
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯 | 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤280 | b |
三档 | x>280 | 0.82 |
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com