
【题目】一次函数 ![]() 和
和 ![]() 同一直角坐标系内的图象是( )
同一直角坐标系内的图象是( )
A.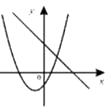
B.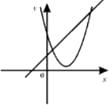
C.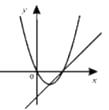
D.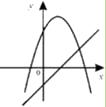
【答案】C
【解析】A.由抛物线知,a>0,b>0;由直线知a<0,b>0,a的值矛盾,A不符合题意;
B.由抛物线知,a>0,b<0;由直线知a>0,b>0,b的值矛盾,B不符合题意;
C.由抛物线知,a>0,b<0;由直线知a>0,b<0,两结论一致,C符合题意;
D.由抛物线知,a<0,b>0;由直线知a>0,b<0,a、b的值矛盾,D不符合题意.
所以答案是:C.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对二次函数图象以及系数a、b、c的关系的理解,了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题: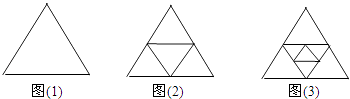
在第n个图形中有个三角形(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了![]() 本,有两种规格,单价分别为
本,有两种规格,单价分别为![]() 元和
元和![]() 元去时我领了
元去时我领了![]() 元,现在找回
元,现在找回![]() 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为![]() 元的笔记本
元的笔记本![]() 本,试用含
本,试用含![]() 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元
(3)如果小赵的零用钱数目是整数,且少于![]() 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=﹣![]() x+2的图象分别与x轴、y轴交于点A、B.
x+2的图象分别与x轴、y轴交于点A、B.
(1)请直接写出A,B两点坐标:A 、B
(2)在直角坐标系中画出函数图象;
(3)若平面内有一点C(5,3),请连接AC、BC,则△ABC是 三角形.
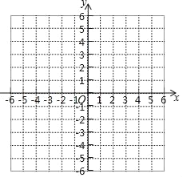
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,上面分别写着0,π, ![]() ,
, ![]() ,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(3ab-4)(3ab+4);
(2)(![]() π+
π+![]() )(
)(![]() π-
π-![]() );
);
(3)(-0.3x+0.2y)(-0.3x-0.2y);
(4)(![]() x-
x-![]() y)(-
y)(-![]() x-
x-![]() y).
y).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2的坐标为__________,点A2 019的坐标为__________;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时,画了这样一个图,以数轴上的单位长为1的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A,请根据图形回答下列问题:
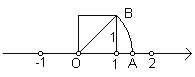
(1)线段OA的长度是___________
(2)这种研究和解决问题的方式,体现了的数学思想方法( ).
A.数形结合B.归纳C.换元D.消元
(3)计算:![]() ﹣
﹣![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com