
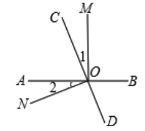
【题目】如图,直线AB、CD相交于O点,OM⊥AB;
(1)若∠1=∠2,求∠NOD;
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】(1)∠NOD=90°;(2)∠AOC=60°;∠MOD=150°
【解析】
(1)根据垂直的定义可得∠AOM=90°,从而得出∠1+∠AOC=90°,然后利用等量代换可得∠2+∠AOC=90°,从而求出结论;
(2)根据垂直的定义可得∠AOM=∠BOM=90°,然后结合已知条件即可求出∠1,然后从而求出结论.
解:(1)∵OM⊥AB
∴∠AOM=90°
∴∠1+∠AOC=90°
∵∠1=∠2
∴∠2+∠AOC=90°
∴∠CON=90°
∴∠NOD=180°-∠CON=90°
(2)∵OM⊥AB
∴∠AOM=∠BOM=90°
∵∠1=![]() ∠BOC
∠BOC
∴∠1=![]() ∠BOM=30°
∠BOM=30°
∴∠AOC=∠AOM-∠1=60°
∴∠MOD=180°-∠1=150°


科目:初中数学 来源: 题型:
【题目】两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
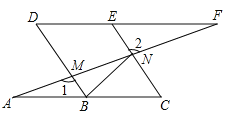
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题: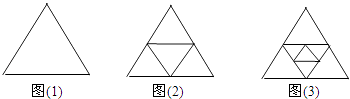
在第n个图形中有个三角形(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
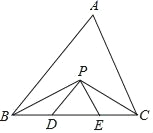
【题目】如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是_____cm,∠DPE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
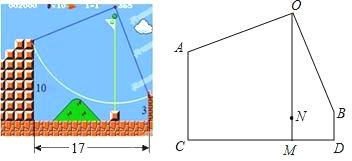
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,玛丽在荡绳索过程中离地面的最低点的高度MN=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了![]() 本,有两种规格,单价分别为
本,有两种规格,单价分别为![]() 元和
元和![]() 元去时我领了
元去时我领了![]() 元,现在找回
元,现在找回![]() 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为![]() 元的笔记本
元的笔记本![]() 本,试用含
本,试用含![]() 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元
(3)如果小赵的零用钱数目是整数,且少于![]() 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com