
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.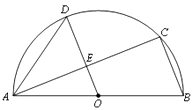
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
【答案】
(1)解:∵AB是半圆的直径,
∴∠C=90°,
∵OD∥BC,
∴∠OEA=∠C=90°,∠AOD=∠B=70°,
∵OA=0D,
∴∠D=∠OAD= ![]() ,
,
∴在Rt△ADE中,∠DAC=90°-55°=35°.
(2)解:∵∠OEA=90°,
∴OE⊥AC,
∴AE= ![]() AC=1.5,
AC=1.5,
∵AB=4,
∴AO=OD=2,
∴在Rt△AEO中,OE= ![]() ,
,
∴DE=OD-OE= ![]() .
.
【解析】(1)根据直径所对的圆周角是直角得出∠C=90°,再根据OD∥BC,证出∠AOD=∠B=70°及∠OEA=90°,再求出∠D的度数,根据三角形的内角和定理即可求出∠DAC的度数。
(2)由(1)的证明过程可知OE⊥AC,先根据垂径定理得出AE的长,再在Rt△AEO中,利用勾股定理求出OE的长,然后根据DE=OD-OE,求出结果。
【考点精析】关于本题考查的三角形的内角和外角和勾股定理的概念,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,六边形![]() 的内角都相等,
的内角都相等,![]() ,则下列结论成立的个数是
,则下列结论成立的个数是
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形;⑤六边形
是平行四边形;⑤六边形![]() 即是中心对称图形,又是轴对称图形( )
即是中心对称图形,又是轴对称图形( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
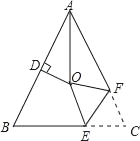
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,玛丽在荡绳索过程中离地面的最低点的高度MN=_____.
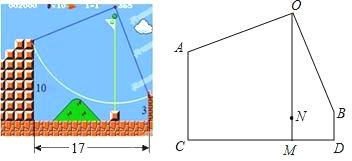
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 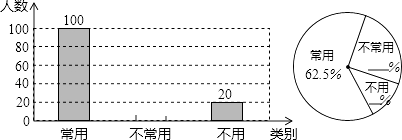
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
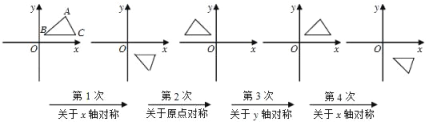
【题目】如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2018次变换后所得的A点坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com