
【题目】如图,六边形![]() 的内角都相等,
的内角都相等,![]() ,则下列结论成立的个数是
,则下列结论成立的个数是
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形;⑤六边形
是平行四边形;⑤六边形![]() 即是中心对称图形,又是轴对称图形( )
即是中心对称图形,又是轴对称图形( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
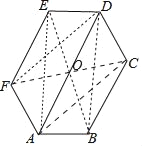
【解析】试题解析:∵六边形ABCDEF的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,
∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,
∴AD∥EF∥CB,故②正确,
∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,
∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA是等腰梯形,
∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,
连接CF与AD交于点O,连接DF、AC、AE、DB、BE.
∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC是平行四边形,故④正确,
同法可证四边形AEDB是平行四边形,∴AD与CF,AD与BE互相平分,∴OF=OC,OE=OB,OA=OD,
∴六边形ABCDEF既是中心对称图形,故⑤正确,
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,连接对角线BD,作AE⊥BD于E,CF⊥BD于F, 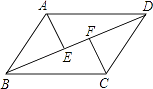
(1)求证:△AED≌△CFB;
(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
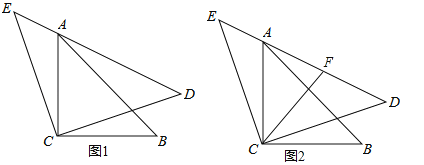
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
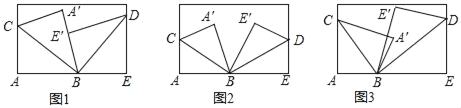
【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
小明发现,可以设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
利用方程组可以解决.
请回答:
另一个因式为 ,m的值为 ;
参考小明的方法,解决下面的问题:
已知二次三项式2x2+3x﹣k有一个因式是(x﹣4),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )

A. 12 B. 13 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是中华民族古老的传统节日.甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案.
甲超市方案:购买该种粽子超过200元后,超出200元的部分按95%收费;
乙超市方案:购买该种粽子超过300元后,超出300元的部分按90%收费.
设某位顾客购买了x元的该种粽子.
(1)补充表格,填写在“横线”上:
(2)列式计算说明,如果顾客在“端午节”当天购买该种粽子超过200元,那么到哪家超市花费更少?
x (单位:元) | 实际在甲超市的花费 (单位:元) | 实际在乙超市的花费 (单位:元) |
0<x≤200 | x | x |
200<x≤300 | x | |
x>300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )
A.y3>y1>y2
B.y1>y3>y2
C.y3>y2>y1
D.y1>y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.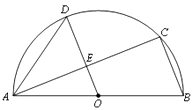
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com