
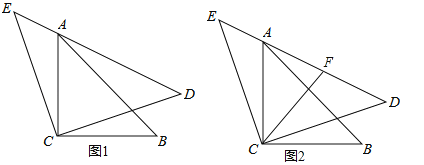
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接BD,根据题意可以证明△ADB是直角三角形,然后根据三角形全等和勾股定理即可证明结论成立;
(2)过C作CM⊥ED于M.根据(1)中的结论得到AD的长,从而得到ED的长,根据等腰三角形的性质得到CM和MD的长,根据中点的性质及线段的和差得到MF的长.在Rt△CMF中,根据勾股定理即可得到结论.
(1)连接BD.
∵△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,∴∠ECA+∠ACD=∠ACD+∠DCB=90°,∠CEA=∠CDE=45°,∠CAB=∠CBA=45°,∴∠ECA=∠DCB.
在△ECA和△DCB中,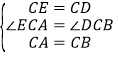 ,∴△ECA≌△DCB(SAS),∴AE=BD,∠CEA=∠CDB,∴∠ADB=∠CDB+∠EDC=90°,∴△ADB是直角三角形,∴AD2+BD2=AB2.
,∴△ECA≌△DCB(SAS),∴AE=BD,∠CEA=∠CDB,∴∠ADB=∠CDB+∠EDC=90°,∴△ADB是直角三角形,∴AD2+BD2=AB2.
在Rt△ACB中,AC=BC,AC2+BC2=2AC2=AB2,∴2AC2=AD2+BD2,即AE2+AD2=2AC2;
(2)过C作CM⊥ED于M.
∵AE2+AD2=2AC2,AE=3,AC=![]() ,∴AD=9,∴ED=EA+AD=3+9=12.
,∴AD=9,∴ED=EA+AD=3+9=12.
∵点F是AD的中点,∴AF=DF=4.5.
∵△ECD是等腰直角三角形,∴CM=![]() ED=MD=6,∴MF=MD-DF=6-4.5=1.5.在Rt△CMF中,CF=
ED=MD=6,∴MF=MD-DF=6-4.5=1.5.在Rt△CMF中,CF=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度![]() 元收费,如果超过140度,超过部分按每度
元收费,如果超过140度,超过部分按每度![]() 元收费.
元收费.
![]() 若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
![]() 若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
![]() 若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
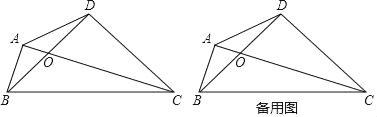
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求![]() 的值;
的值;
(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造![]() 个新公共自行车站点和配置
个新公共自行车站点和配置![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形![]() 的内角都相等,
的内角都相等,![]() ,则下列结论成立的个数是
,则下列结论成立的个数是
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形;⑤六边形
是平行四边形;⑤六边形![]() 即是中心对称图形,又是轴对称图形( )
即是中心对称图形,又是轴对称图形( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com