
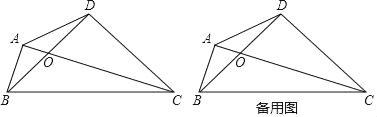
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求![]() 的值;
的值;
(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
【答案】(1)ACD;(2)![]() ;(3)AD⊥AN,
;(3)AD⊥AN,![]() .
.
【解析】
(1)因为∠BAC=∠BDC=90°,得到∠ABD+∠AOB=90°,∠ACD+∠COD=90°,根据等角的余角相等,即可得到∠ABD=∠ACD.
(2)作DH⊥OC于H.证明△BAO≌△DHO,根据全等三角形的性质得到AB=DH,设OD=OB=a,则BD=CD=2a,根据等面积法求出DH的长度,即可求出![]() 的值;
的值;
(3)连接BN、CN.根据△BDC是等腰直角三角形,得到D、N关于BC对称,有O′A=O′D=O′N=O′B=O′C,得到A、B、N、C、D五点共圆,根据圆周角定理得到∠AND=∠ACD,即可求出![]()
解:(1)∵∠BAC=∠BDC=90°,
∴∠ABD+∠AOB=90°,∠ACD+∠COD=90°,
∵∠AOB=∠COD,
∴∠ABD=∠ACD.
故答案为ACD.
(2)作DH⊥OC于H.
∵∠BAO=∠DHO=90°,∠AOB=∠DOH,OB=OD,
∴△BAO≌△DHO,
∴AB=DH,设OD=OB=a,则BD=CD=2a,![]()
∴![]()
(3)结论:AD⊥AN, ![]()
理由:连接BN、CN.
∵△BDC是等腰直角三角形,
D、N关于BC对称,
∴四边形DBNC是正方形,设BC的中点为O′,连接O′N、O′A、O′D.
则有O′A=O′D=O′N=O′B=O′C,
∴A、B、N、C、D五点共圆,
∵DN是⊙O′的直径,
∴∠DAN=90°,
∴AD⊥AN,
∵∠AND=∠ACD,
∴tan∠AND=tan∠ACD,
∴![]()


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
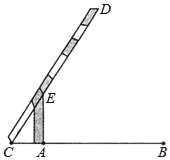
【题目】如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.3m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率= ![]() =
= ![]() ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
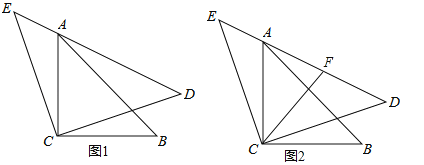
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
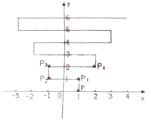
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位到达
,第3次向上跳动1个单位到达![]() ,第4次向右跳动3个单位到达
,第4次向右跳动3个单位到达![]() ,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点
,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点![]() 的坐标为( ).
的坐标为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
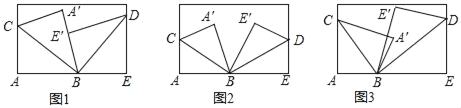
【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是( )

A. 12 B. 13 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为 ![]() 。
。
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com