
【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为 ![]() 。
。
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率。
【答案】
(1)解:设有红球 ![]() 个,由题意可得;
个,由题意可得; ![]() ,解得
,解得 ![]() ,即布袋中红球有1个;
,即布袋中红球有1个;
(2)解:画树状图如下:一共有12种等可能情况,其中两次都摸到白球的有2次,
∴ P(两次都是白球)= ![]() .
.

【解析】根据白球的概率=![]() ,建立方程求解即可。
,建立方程求解即可。
(2)抓住已知摸出1个球后不放回,再摸出1个球,列出树状图,求出所有等可能的结果数,再求出两次都摸到白球的可能数,利用概率公式求出结果。
【考点精析】掌握列表法与树状图法和概率公式是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
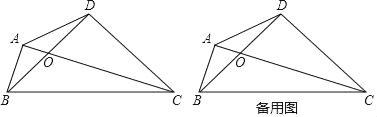
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求![]() 的值;
的值;
(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图.
(1)在![]() 的内部任取一个点E,过点E作EM⊥OB;
的内部任取一个点E,过点E作EM⊥OB;
(2)在边![]() 上取一点N,作NF⊥OA于点N,且NF=EM;
上取一点N,作NF⊥OA于点N,且NF=EM;
(3)过点E作直线l1∥OB,过点F作直线l2∥OA,l1 与l2交于点![]() ;
;
(4)画射线![]() .
.
则射线![]() 为
为![]() 的平分线.
的平分线.

根据小明的画法回答下面的问题:
(1)小明作l1∥OB,l2∥OA的目的是___________________________________________;
(2)l1 与l2交于点![]() ,则射线
,则射线![]() 为
为![]() 的平分线的依据是__________________________.
的平分线的依据是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
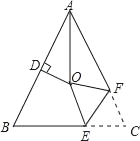
【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 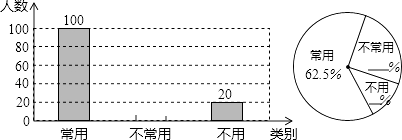
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=5 cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设落点为F,若△ABF的面积为30 cm2,求△ADE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com