Question

【题目】小明在没有量角器和圆规的情况下，利用刻度尺和一副三角板画出了一个角的平分线，他的做法是这样的：如图.

（1）在的内部任取一个点E，过点E作EM⊥OB；

（2）在边上取一点N，作NF⊥OA于点N，且NF=EM；

（3）过点E作直线l1∥OB，过点F作直线l2∥OA，l1 与l2交于点；

（4）画射线．

则射线为的平分线．

根据小明的画法回答下面的问题：

（1）小明作l1∥OB，l2∥OA的目的是___________________________________________；

（2）l1 与l2交于点，则射线为的平分线的依据是__________________________．

Answer 1

【答案】利用平行线间的距离处处相等 到角两边距离相等的点在角的平分线上.

【解析】

（1）作l1∥OB，l2∥OA的目的是：利用平行线间的距离处处相等；

（2）过点P作PG⊥OA于G，PH⊥OB于H,再根据l1∥OB，EM⊥OB得出PH= EM;再根据 l2∥OA，NF⊥OA,得出PG=FN，再根据NF=EM，得出PG=PH,根据到角两边距离相等的点在角的平分线上，从而得出射线为的平分线.

（1）作l1∥OB，l2∥OA的目的是利用平行线间的距离处处相等；

故答案为: 利用平行线间的距离处处相等；

（2）过点P作PG⊥OA于G，PH⊥OB于H,

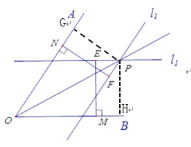
∵l1∥OB，EM⊥OB，∴PH= EM;

∵l2∥OA，NF⊥OA, ∴PG=FN

∵NF=EM，∴PG=PH,

∴射线为的平分线(到角两边距离相等的点在角的平分线上).

故答案为: 到角两边距离相等的点在角的平分线上.