
【题目】(1)根据下表回答:
| 1 | 1.7 | 1.73 | 1.74 | 1.8 | 2 |
| 1 | 2.89 | 2.9929 | 3.0276 | 3.24 | 4 |
①![]() 的平方根是_____________;
的平方根是_____________;
②由表可知,![]() 在表中哪两个相邻的数之间(小数部分是两位小数)?
在表中哪两个相邻的数之间(小数部分是两位小数)?
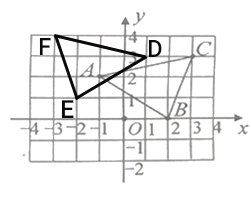
(2)如图,在平面直角坐标系中,已知三点![]()
![]()

①三角形![]() 的面积是_______
的面积是_______
②分别将![]() 三点的横坐标乘
三点的横坐标乘![]() ,纵坐标加
,纵坐标加![]() ,记坐标变换后
,记坐标变换后![]() 所对的点分别为
所对的点分别为![]() 在坐标系中画出以这三点为顶点的三角形
在坐标系中画出以这三点为顶点的三角形![]()
【答案】(1) ①![]() ;②
;②![]() 在1.73与1.74之间;
在1.73与1.74之间;
(2) ①5.5;②见解析;
【解析】
(1) ①根据平方根的定义,由表格的信息即可得到;
②观察表格的数据,即可得到答案;
(2) ①先观察三角形在直角坐标系中的位置,再用一个矩形的面积减掉多余的三角形的面积即可得到;
②根据题意做变换,即可得到![]() 点变换后的坐标,再在直角坐标系中画出来即可;
点变换后的坐标,再在直角坐标系中画出来即可;
解:(1)①由表格可以看出![]() 所对应的x值为1.8
所对应的x值为1.8
∴3.24的平方根是![]()
②由表格可知,![]() 在1.73与1.74之间.
在1.73与1.74之间.
(2)①![]()
故答案为5.5
②D点横坐标为:![]() ,纵坐标为:
,纵坐标为:![]()
∴![]()
E点横坐标为:![]() ,纵坐标为:
,纵坐标为:![]()
∴![]()
F点横坐标为:![]() ,纵坐标为:
,纵坐标为:![]()
∴![]()
根据得到的点![]() 的坐标在坐标系中画出以这三点为顶点的三角形
的坐标在坐标系中画出以这三点为顶点的三角形![]() 如下图:
如下图:


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】小明在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图.
(1)在![]() 的内部任取一个点E,过点E作EM⊥OB;
的内部任取一个点E,过点E作EM⊥OB;
(2)在边![]() 上取一点N,作NF⊥OA于点N,且NF=EM;
上取一点N,作NF⊥OA于点N,且NF=EM;
(3)过点E作直线l1∥OB,过点F作直线l2∥OA,l1 与l2交于点![]() ;
;
(4)画射线![]() .
.
则射线![]() 为
为![]() 的平分线.
的平分线.

根据小明的画法回答下面的问题:
(1)小明作l1∥OB,l2∥OA的目的是___________________________________________;
(2)l1 与l2交于点![]() ,则射线
,则射线![]() 为
为![]() 的平分线的依据是__________________________.
的平分线的依据是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 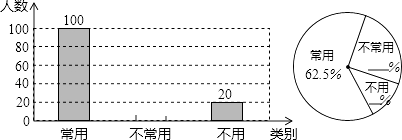
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ ![]() 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为 ![]() ,请用含
,请用含 ![]() 的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 ![]() 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
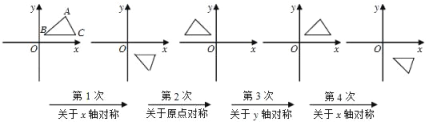
【题目】如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2018次变换后所得的A点坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=5 cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设落点为F,若△ABF的面积为30 cm2,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
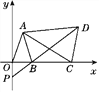
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解. 根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有个,分别为;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com