
”¾ĢāÄæ”æ¼Ń¼ŃĻņĢ½¾æŅ»ŌŖČż“Ī·½³Ģx3+2x2©x©2=0µÄ½āµÄĒéæö£¬øł¾ŻŅŌĶłµÄѧĻ°¾Ń飬ĖūĻėµ½ĮĖ·½³ĢÓėŗÆŹżµÄ¹ŲĻµ£¬Ņ»“ĪŗÆŹży=kx+b£Øk”Ł0£©µÄĶ¼ĻóÓėxÖį½»µćµÄŗį×ų±ź¼“ĪŖŅ»ŌŖŅ»“Ī·½³Ģkx+b£Øk”Ł0£©µÄ½ā£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóÓėxÖį½»µćµÄŗį×ų±ź¼“ĪŖŅ»ŌŖ¶ž“Ī·½³Ģax2+bx+c=0£Øa”Ł0£©µÄ½ā£¬Čē£ŗ¶ž“ĪŗÆŹży=x2©2x©3µÄĶ¼ĻóÓėxÖįµÄ½»µćĪŖ£Ø©1£¬0£©ŗĶ£Ø3£¬0£©£¬½»µćµÄŗį×ų±ź©1ŗĶ3¼“ĪŖx2©2x©3=0µÄ½ā£® øł¾ŻŅŌÉĻ·½³ĢÓėŗÆŹżµÄ¹ŲĻµ£¬Čē¹ūĪŅĆĒÖ±µ½ŗÆŹży=x3+2x2©x©2µÄĶ¼ĻóÓėxÖį½»µćµÄŗį×ų±ź£¬¼“æÉÖŖ·½³Ģx3+2x2©x©2=0µÄ½ā£®
¼Ń¼ŃĪŖĮĖ½āŗÆŹży=x3+2x2©x©2µÄĶ¼Ļó£¬ĶعżĆčµć·Ø»³öŗÆŹżµÄĶ¼Ļó£®
x | ” | ©3 | © | ©2 | © | ©1 | © | 0 |
| 1 |
| 2 | ” |
y | ” | ©8 | © | 0 |
| m | © | ©2 | © | 0 |
| 12 | ” |
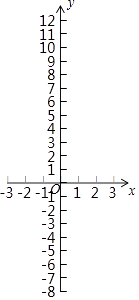
£Ø1£©Ö±½ÓŠ“³ömµÄÖµ£¬²¢»³öŗÆŹżĶ¼Ļó£»
£Ø2£©øł¾Ż±ķøńŗĶĶ¼ĻóæÉÖŖ£¬·½³ĢµÄ½āÓŠøö£¬·Ö±šĪŖ£»
£Ø3£©½čÖśŗÆŹżµÄĶ¼Ļó£¬Ö±½ÓŠ“³ö²»µČŹ½x3+2x2£¾x+2µÄ½ā¼Æ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗÓÉĢāŅām=©1+2+1©2=0£®
ŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®
£Ø2£©3£»©2,»ņ©1»ņ1
£Ø3£©½ā£ŗ²»µČŹ½x3+2x2£¾x+2µÄ½ā¼Æ£¬¼“ĪŖŗÆŹży=x3+2x2©x©2µÄŗÆŹżÖµ“óÓŚ0µÄ×Ō±äĮæµÄȔֵ·¶Ī§£®
¹Ū²ģĶ¼ĻóæÉÖŖ£¬©2£¼x£¼©1»ņx£¾1
”¾½āĪö”æ½ā£ŗ£Ø1£©ÓÉĢāŅām=©1+2+1©2=0£®
ŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®
 £»£Ø2£©øł¾Ż±ķøńŗĶĶ¼ĻóæÉÖŖ£¬·½³ĢµÄ½āÓŠ3øö£¬·Ö±šĪŖ©2£¬»ņ©1»ņ1£®
£»£Ø2£©øł¾Ż±ķøńŗĶĶ¼ĻóæÉÖŖ£¬·½³ĢµÄ½āÓŠ3øö£¬·Ö±šĪŖ©2£¬»ņ©1»ņ1£®
ĖłŅŌ“š°øŹĒ3£¬©2£¬»ņ©1»ņ1£®
”¾æ¼µć¾«Īö”æ¹ŲÓŚ±¾Ģāæ¼²éµÄ¶ž“ĪŗÆŹżµÄĶ¼ĻóŗĶÅ×ĪļĻßÓė×ų±źÖįµÄ½»µć£¬ŠčŅŖĮĖ½ā¶ž“ĪŗÆŹżĶ¼Ļń¹Ų¼üµć£ŗ1”¢æŖæŚ·½Ļņ2”¢¶Ō³ĘÖį 3”¢¶„µć 4”¢ÓėxÖį½»µć 5”¢ÓėyÖį½»µć£»Ņ»ŌŖ¶ž“Ī·½³ĢµÄ½āŹĒĘä¶ŌÓ¦µÄ¶ž“ĪŗÆŹżµÄĶ¼ĻńÓėxÖįµÄ½»µć×ų±ź£®Ņņ“ĖŅ»ŌŖ¶ž“Ī·½³ĢÖŠµÄb2-4ac£¬ŌŚ¶ž“ĪŗÆŹżÖŠ±ķŹ¾Ķ¼ĻńÓėxÖįŹĒ·ńÓŠ½»µć£®µ±b2-4ac>0Ź±£¬Ķ¼ĻńÓėxÖįÓŠĮ½øö½»µć£»µ±b2-4ac=0Ź±£¬Ķ¼ĻńÓėxÖįÓŠŅ»øö½»µć£»µ±b2-4ac<0Ź±£¬Ķ¼ĻńÓėxÖįƻӊ½»µć£®²ÅÄÜµĆ³öÕżČ·“š°ø£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©øł¾ŻĻĀ±ķ»Ų“š£ŗ
| 1 | 1.7 | 1.73 | 1.74 | 1.8 | 2 |
| 1 | 2.89 | 2.9929 | 3.0276 | 3.24 | 4 |
¢Ł![]() µÄĘ½·½øłŹĒ_____________£»
µÄĘ½·½øłŹĒ_____________£»
¢ŚÓɱķæÉÖŖ£¬![]() ŌŚ±ķÖŠÄÄĮ½øöĻąĮŚµÄŹżÖ®¼ä£ØŠ”Źż²æ·ÖŹĒĮ½Ī»Š”Źż£©£æ
ŌŚ±ķÖŠÄÄĮ½øöĻąĮŚµÄŹżÖ®¼ä£ØŠ”Źż²æ·ÖŹĒĮ½Ī»Š”Źż£©£æ
£Ø2£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖČżµć![]()
![]()

¢ŁČż½ĒŠĪ![]() µÄĆ껿ŹĒ_______
µÄĆ껿ŹĒ_______
¢Ś·Ö±š½«![]() ČżµćµÄŗį×ų±ź³Ė
ČżµćµÄŗį×ų±ź³Ė![]() £¬×Ż×ų±ź¼Ó
£¬×Ż×ų±ź¼Ó![]() £¬¼Ē×ų±ź±ä»»ŗó
£¬¼Ē×ų±ź±ä»»ŗó![]() Ėł¶ŌµÄµć·Ö±šĪŖ
Ėł¶ŌµÄµć·Ö±šĪŖ![]() ŌŚ×ų±źĻµÖŠ»³öŅŌÕāČżµćĪŖ¶„µćµÄČż½ĒŠĪ
ŌŚ×ų±źĻµÖŠ»³öŅŌÕāČżµćĪŖ¶„µćµÄČż½ĒŠĪ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
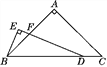
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬AB£½AC£¬”ĻBAC£½90”ć£¬µćDŌŚĻ߶ĪBCÉĻ£¬”ĻEDB£½![]() ”ĻC£¬BE”ĶDE£¬“¹×ćĪŖE£¬DEÓėABĻą½»ÓŚµćF.ŹŌĢ½¾æĻ߶ĪBEÓėDFµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
”ĻC£¬BE”ĶDE£¬“¹×ćĪŖE£¬DEÓėABĻą½»ÓŚµćF.ŹŌĢ½¾æĻ߶ĪBEÓėDFµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
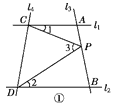
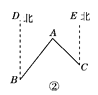
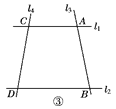
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŅŃÖŖÖ±Ļßl1”Īl2£¬ĒŅl3ŗĶl1£¬l2·Ö±šĻą½»ÓŚA£¬BĮ½µć£¬l4ŗĶl1£¬l2·Ö±š½»ÓŚC£¬DĮ½µć£¬”ĻACP£½”Ļ1£¬”ĻBDP£½”Ļ2£¬”ĻCPD£½”Ļ3£¬
µćPŌŚĻ߶ĪABÉĻ£®
(1)Čō”Ļ1£½22”ć£¬”Ļ2£½33”ć£¬Ōņ”Ļ3£½________£»
(2)ŹŌÕŅ³ö”Ļ1£¬”Ļ2£¬”Ļ3Ö®¼äµÄµČĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
(3)Ó¦ÓĆ(2)ÖŠµÄ½įĀŪ½ā“šĻĀĮŠĪŹĢā£»
ČēĶ¼¢Ś£¬µćAŌŚB“¦±±Ę«¶«40”ćµÄ·½ĻņÉĻ£¬ŌŚC“¦µÄ±±Ę«Ī÷45”ćµÄ·½ĻņÉĻ£¬Ēó”ĻBACµÄ¶ČŹż£»
(4)Čē¹ūµćPŌŚÖ±Ļßl3ÉĻĒŅŌŚA£¬BĮ½µćĶā²ąŌĖ¶ÆŹ±£¬ĘäĖūĢõ¼ž²»±ä£¬ŹŌĢ½¾æ”Ļ1£¬”Ļ2£¬”Ļ3Ö®¼äµÄ¹ŲĻµ(µćPŗĶA£¬BĮ½µć²»ÖŲŗĻ)£¬Ö±½ÓŠ“³ö½įĀŪ¼“æÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠĪŖĢį³«½ŚŌ¼ÓĆĖ®£¬×¼±øŹµŠŠ×ŌĄ“Ė®”°½×ĢŻ¼Ę·Ń”±·½Ź½£¬ÓĆ»§ÓĆĖ®²»³¬³ö»ł±¾ÓĆĖ®ĮæµÄ²æ·ÖĻķŹÜ»ł±¾¼Ūøń£¬³¬³ö»ł±¾ÓĆĖ®ĮæµÄ²æ·ÖŹµŠŠ¼Ó¼ŪŹÕ·Ń£¬ĪŖøüŗƵŲ×ö¾ö²ß£¬×ŌĄ“Ė®¹«Ė¾Ė껜³éČ”²æ·ÖÓĆ»§µÄÓĆĖ®ĮæŹż¾Ż£¬²¢»ęÖĘĮĖČēĶ¼²»ĶźÕūµÄĶ³¼ĘĶ¼£ØĆæ×鏿¾Ż°üĄØÓŅ¶Ėµćµ«²»°üĄØ×ó¶Ėµć£©£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©“Ė“Ī³éŃłµ÷²éµÄŃł±¾ČŻĮæŹĒ £®
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£®
£Ø3£©Čē¹ū×ŌĄ“Ė®¹«Ė¾½«»ł±¾ÓĆĖ®Įæ¶ØĪŖĆ滧25¶Ö£¬ÄĒĆ“øƵŲĒų6ĶņÓĆ»§ÖŠŌ¼ÓŠ¶ąÉŁÓĆ»§µÄÓĆĖ®Č«²æĻķŹÜ»ł±¾¼Ūøń£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»×ŖÅĢÖŠÓŠA”¢BĮ½øöĒųÓņ£¬AĒųÓņĖł¶ŌµÄŌ²ŠÄ½ĒĪŖ120”ć£¬ČĆ×ŖÅĢ×ŌÓÉ×Ŗ¶ÆĮ½“Ī£®ĄūÓĆŹ÷דĶ¼»ņĮŠ±ķĒó³öĮ½“ĪÖøÕė¶¼ĀäŌŚAĒųÓņµÄøÅĀŹ”£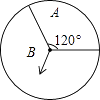
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬PŹĒCD±ßÉĻŅ»µć£¬ĒŅAPŗĶBP·Ö±šĘ½·Ö”ĻDABŗĶ”ĻCBA£¬ČōAD=5£¬AP=8£¬Ōņ”÷APBµÄÖܳ¤ŹĒ £®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻC=90”ć£¬AC=3£¬BC=4£¬PŹĒŠ±±ßABÉĻŅ»¶Æµć£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬PQ”ĶAB½»”÷ABCµÄÖ±½Ē±ßÓŚµćQ£¬ÉčAPĪŖx£¬”÷APQµÄĆ껿ĪŖy£¬ŌņĻĀĮŠĶ¼ĻóÖŠ£¬ÄܱķŹ¾y¹ŲÓŚxµÄŗÆŹż¹ŲĻµµÄĶ¼Ļó“óÖĀŹĒ£Ø £©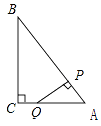
A.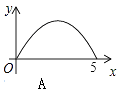
B.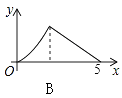
C.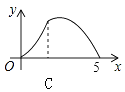
D.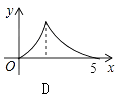
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¹żŌµćOµÄÖ±ĻßÓėĖ«ĒśĻßy= ![]() ½»ÓŚA”¢BĮ½µć£¬¹żµćB×÷BC”ĶxÖį£¬“¹×ćĪŖC£¬Į¬½ÓAC£¬ČōS”÷ABC=5£¬ŌņkµÄÖµŹĒ£Ø £©
½»ÓŚA”¢BĮ½µć£¬¹żµćB×÷BC”ĶxÖį£¬“¹×ćĪŖC£¬Į¬½ÓAC£¬ČōS”÷ABC=5£¬ŌņkµÄÖµŹĒ£Ø £© 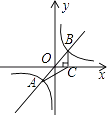
A.![]()
B.![]()
C.5
D.10
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com