
【题目】已知:如图,在平行四边形ABCD中,连接对角线BD,作AE⊥BD于E,CF⊥BD于F, 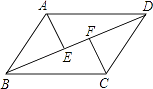
(1)求证:△AED≌△CFB;
(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四边形ABCD的周长.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
又∵AE⊥BD于E,CF⊥BD于F,
∴∠AED=∠CFB=90°,
在△AED和△CFB中,
 ,
,
∴△AED≌△CFB (AAS)
(2)解:在Rt△AED中,
∵∠ADE=30°,AE=3,
∴AD=2AE=2×3=6,
∵∠ABC=75°,∠ADB=∠CBD=30°
∴∠ABE=45°,
在Rt△ABE中,
∵ ![]() =sin45°,
=sin45°,
∴AB= ![]() =3
=3 ![]() ,
,
∴平行四边形ABCD的周长l=2(AB+AD)=2×(6+3 ![]() )=12+6
)=12+6 ![]()
【解析】(1)在平行四边形ABCD中,AD=BC,AD∥BC,可知∠ADE=∠CBD,然后根据AE⊥BD于E,CF⊥BD于F,可知∠AED=∠CFB=90°,根据这三个条件即可证明全等;(2)根据已知∠ABC=75°,∠ADB=30°,AE=3,分别在Rt△ABE、Rt△AED中求出AB、AD的长度,即可求出周长.
【考点精析】利用平行四边形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)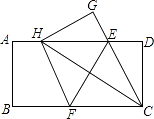
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度![]() 元收费,如果超过140度,超过部分按每度
元收费,如果超过140度,超过部分按每度![]() 元收费.
元收费.
![]() 若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
![]() 若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
![]() 若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形![]() 的内角都相等,
的内角都相等,![]() ,则下列结论成立的个数是
,则下列结论成立的个数是
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形;⑤六边形
是平行四边形;⑤六边形![]() 即是中心对称图形,又是轴对称图形( )
即是中心对称图形,又是轴对称图形( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com