
【题目】如图在平面直角坐标系XOY中,一次函数y=kx-k的图象经过A(2,2),与x轴、y轴分别交于点C、点B.
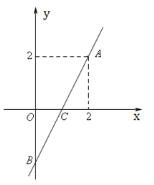
(1)观察图像,直接写出使y≥0的x的取值范围;
(2)求一次函数的解析式;
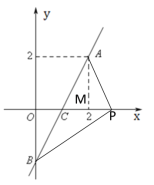
(3)若点P是x轴上一点,且满足△PAB的面积是6,请求出点P的坐标.
【答案】(1)x≥1;(2)y=2x-2;(3)(﹣2,0)或(4,0).
【解析】
(1)先根据一次函数解析式求出C点坐标,观察图像可知:在点C右侧的部分的函数值y≥0,从而求出x的取值范围;
(2)将A点坐标代入即可;
(3)先求出B点的坐标,根据A、B的坐标即可求出OB和AM的长,设P点坐标为(a,0),则PC=![]() ,然后根据S△PAC+S△PBC= S△PAB,列出方程求a即可.
,然后根据S△PAC+S△PBC= S△PAB,列出方程求a即可.
解:(1)∵一次函数y=kx-k的图象与x轴交于点C
∴当y=0时,解得x=1
∴C点坐标为(1,0)
由图像可知:在点C右侧的部分的函数值y≥0
∴此时x≥1
(2)将A(2,2)代入解析式y=kx-k中,得:2=2k-k
解得:k=2
∴一次函数的解析式为:y=2x-2
(3)∵一次函数y=2x-2与y轴交于点B
当x=0时,y=﹣2
∴B点坐标为(0,﹣2)
∴OB=2,AM=2
设P点坐标为(a,0)
∴PC=![]()
∵S△PAC+S△PBC= S△PAB
即![]() PC·AM+
PC·AM+![]() PC·BO=6
PC·BO=6
∴![]()
![]() ·2+
·2+![]()
![]() ·2=6
·2=6
解得:a=﹣2或4
故P点坐标为:(﹣2,0)或(4,0)


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=∠ECD=90°,AC=BC,EC=DC,点D在AB边上.

(1)求证:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.

(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 平面直角坐标系中,过点C(28,28)分别作x轴、y轴的垂线,垂足分别为B、A,一次函数y=![]() x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
x+3的图像分别与x轴和CB交于点D、E,点P 是DE中点,连接AP.
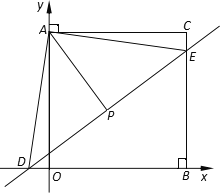
⑴ 求点D与点E的坐标; ⑵求证:△ADO≌△AEC;⑶ 求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲.乙两种商品原来的单价分别为x元.y元,则可列方程组为_________________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com