
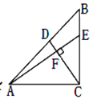
【题目】如图,在Rt△ABC中,∠ACB=900,AC=10,点E在边CB上,CE=![]() ,点D在边AB的中点上,CD⊥AE,垂足为F,则AB的长=__
,点D在边AB的中点上,CD⊥AE,垂足为F,则AB的长=__
【答案】![]()
【解析】
取BC的中点G,连接DG,根据中位线的性质可得:DG∥AC,DG=![]() ,然后利用勾股定理即可求出AE,再利用△ACE面积的两种求法求出CF,利用勾股定理即可求出EF,然后利用相似三角形的判定即可证出:△DCG∽△ECF,列出比例式即可求出DC,最后根据直角三角形斜边上的中线等于斜边的一半即可求出AB的长.
,然后利用勾股定理即可求出AE,再利用△ACE面积的两种求法求出CF,利用勾股定理即可求出EF,然后利用相似三角形的判定即可证出:△DCG∽△ECF,列出比例式即可求出DC,最后根据直角三角形斜边上的中线等于斜边的一半即可求出AB的长.
解:取BC的中点G,连接DG,
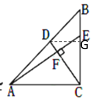
∵点D在边AB的中点
∴DG是△ABC的中位线
∴DG∥AC,DG=![]()
∴∠DGC=90°
根据勾股定理:AE=![]()
∵S△ACE=![]()
解得:CF=6
根据勾股定理:EF=![]()
∵∠DCG=∠ECF,∠DGC=∠EFC=90°
∴△DCG∽△ECF
∴![]()
∴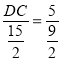
解得:DC=![]()
在Rt△ABC中,AB=2CD=![]()
故答案为![]()


科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C、O、A都不重合),过点A、C分别向直线BM作垂线段,垂足分别为E、F,连接OE,OF.


(1)①依据题意补全图形;
②猜想OE与OF的数量关系为_________________.
(2)小东通过观察、实验发现点M在射线CA上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明(1)中猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与△OAE全等的三角形,从而得到相等的线段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组△OAB和△EAB,再依据直角三角形斜边中线的性质,菱形四边相等,可以构造一对以OE和OF为对应边的全等三角形,即可证明猜想.
……
请你参考上面的想法,帮助小东证明(1)中的猜想(一种方法即可).
(3)当∠ADC=120°时,请直接写出线段CF,AE,EF之间的数量关系是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条![]() ,其中
,其中![]() ,
,![]() .然后在纸条上任意画一条截线段
.然后在纸条上任意画一条截线段![]() ,将纸片沿
,将纸片沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() .如图2所示:
.如图2所示:

探究:
(1)若![]() ,
,![]() ______°;
______°;
(2)改变折痕![]() 位置,
位置,![]() 始终是______三角形,请说明理由;
始终是______三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究![]() 的面积时,发现
的面积时,发现![]() 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出![]() 的面积最小值为
的面积最小值为![]() ,此时
,此时![]() 的大小可以为______°;
的大小可以为______°;
(4)小明继续动手操作,发现了![]() 面积的最大值.请你求出这个最大值.
面积的最大值.请你求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系XOY中,一次函数y=kx-k的图象经过A(2,2),与x轴、y轴分别交于点C、点B.
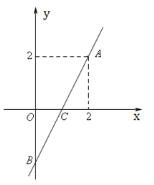
(1)观察图像,直接写出使y≥0的x的取值范围;
(2)求一次函数的解析式;
(3)若点P是x轴上一点,且满足△PAB的面积是6,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件:①∠A=45°,AB=12,AC=15,∠A′=45°,A′B′=16,A′C′=20;②∠A=47°,AB=1.5,AC=2,∠B′=47°,A′B′=2.8,B′C′=2.1;③∠A=47°,AB=2,AC=3,∠B′=47°,A′B′=4,B′C′=6,其中能判定△ABC与△A′B′C′相似的有 ( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
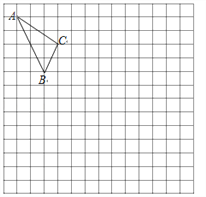
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com