
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.

【答案】9.
【解析】
连接AD,AM,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点A关于直线EF的对称点为点C,MA=MC,推出MC+DM=MA+DM≥AD,故AD的长为BM+MD的最小值,由此即可得出结论.
连接AD,MA.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×6×AD=18,解得AD=6,
×6×AD=18,解得AD=6,
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+![]() BC=6+
BC=6+![]() ×6=6+3=9.
×6=6+3=9.
故答案为:9.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.解答下列问题:

(1)图中a的值为;
(2)当x>1.5(h)时,求甲车行驶路程y(km)与时间x(h)的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列六个命题:①相等的角是对顶角;②两直线平行,同位角相等;③若一个三角形的两个内角分别为![]() 和
和![]() ,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
,则这个三角形是直角三角形;④全等三角形的对应角相等。其中逆命题是假命题的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
科目:初中数学 来源: 题型:
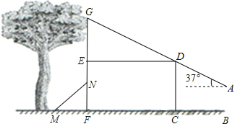
【题目】身高![]() 米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形
米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形![]() 代表建筑物,兵兵位于建筑物前点
代表建筑物,兵兵位于建筑物前点![]() 处,风筝挂在建筑物上方的树枝点
处,风筝挂在建筑物上方的树枝点![]() 处(点
处(点![]() 在
在![]() 的延长线上).经测量,兵兵与建筑物的距离
的延长线上).经测量,兵兵与建筑物的距离![]() 米,建筑物底部宽
米,建筑物底部宽![]() 米,风筝所在点
米,风筝所在点![]() 与建筑物顶点
与建筑物顶点![]() 及风筝线在手中的点
及风筝线在手中的点![]() 在同一条直线上,点
在同一条直线上,点![]() 距地面的高度
距地面的高度![]() 米,风筝线与水平线夹角为
米,风筝线与水平线夹角为![]() .
.
![]() 求风筝距地面的高度
求风筝距地面的高度![]() ;
;
![]() 在建筑物后面有长
在建筑物后面有长![]() 米的梯子
米的梯子![]() ,梯脚
,梯脚![]() 在距墙
在距墙![]() 米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根
米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根![]() 米长的竹竿能否触到挂在树上的风筝?
米长的竹竿能否触到挂在树上的风筝?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
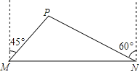
【题目】我市准备在相距![]() 千米的
千米的![]() ,
,![]() 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在![]() 地北偏东
地北偏东![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 处,有一个半径为
处,有一个半径为![]() 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com