
【题目】如图①,![]() 中,
中,![]() ,
,![]() 、∠C的平分线交于
、∠C的平分线交于![]() 点,过
点,过![]() 点作
点作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .试回答:
.试回答:
(1)图中等腰三角形有________个.猜想:![]() 与
与![]() 、
、![]() 之间的关系是________.说明理由;
之间的关系是________.说明理由;
(2)如图②,若![]() ,图中等腰三角形有________个,在第(1)问中
,图中等腰三角形有________个,在第(1)问中![]() 与
与![]() 、
、![]() 间的关系还存在吗?
间的关系还存在吗?
(3)如图③,若![]() 中
中![]() 的平分线
的平分线![]() 与三角形外角平分线
与三角形外角平分线![]() 交于
交于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,这时图中还有等腰三角形吗?
,这时图中还有等腰三角形吗?![]() 与
与![]() 、
、![]() 关系又如何?说明你的理由.
关系又如何?说明你的理由.
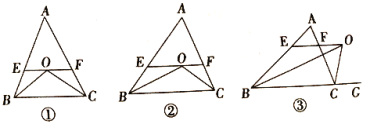
【答案】(1) 5个,![]() ;(2)见解析;(3) 见解析.
;(2)见解析;(3) 见解析.
【解析】
(1)根据等腰三角形的判定、平分线的性质及角平分线可得有5个等腰三角形, 由△EOB和△FOC是等腰三角形,则EO=BE,OF=FC,则EF=BE+FC;
(2)由(1)的证明过程可知:在证△OEB、△OFC是等腰三角形的过程中,与AB=AC的条件没有关系,故这两个等腰三角形还成立.所以(1)中得出的EF=BE+FC的结论仍成立.
(3)思路与(2)相同,只不过结果变成了EF=BE-FC.
解:(1)如图1,图中共有5个等腰三角形,分别是△AEF、△OEB、△OFC、△OBC、△ABC;
理由是:∵AB=AC,
∴∠ACB=∠ABC,△ABC是等腰三角形;
∵BO、CO分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=![]() ∠ABC,∠OCB=∠ACO=
∠ABC,∠OCB=∠ACO=![]() ∠ACB,
∠ACB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠ABO=∠OBC=∠EOB=∠OCB=∠FOC=∠FCO,
∴△EOB、△OBC、△FOC都是等腰三角形,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE,
∴△AEF是等腰三角形,
∴图中是等腰三角形的有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() 、
、![]() 、
、![]() 的关系是
的关系是![]() .理由如下:
.理由如下:
∵![]() 、
、![]() 平分
平分![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
∴![]() .
.
(2)2个
存在(1)的结论仍然成立.(证明过程同(1)).
(3)![]() 和
和![]() 仍是等腰三角形,
仍是等腰三角形,![]() .理由如下:
.理由如下:
同(1)可证得![]() 是等腰三角形.
是等腰三角形.
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,故
,故![]() 是等腰三角形,
是等腰三角形,
∴![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.
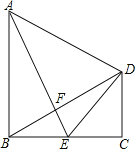
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a2(﹣a4)+2(a2)3
(2)(2x﹣1)(2x+1)﹣(x﹣6)(4x+3)
(3)(2x﹣3y)2+2(y+3x)(3x﹣y)
(4)(a﹣2b+3)(a+2b+3)
(5) ![]()
(6)(2m+3n)(2m﹣n)﹣2n(2m﹣n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
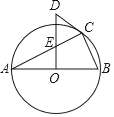
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com