
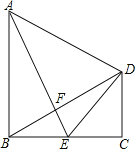
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
【答案】(1)见解析;(2)AE=BD,AE⊥BD,理由见解析;(3)△AED的面积为![]() .
.
【解析】
(1)由已知条件可推导得到![]() ,由SAS即可证明△ABE≌△BCD;
,由SAS即可证明△ABE≌△BCD;
(2)由(1)可得△ABE≌△BCD 可得AE=BD,再由角的转化可得∠AFB=90°,即可证明AE⊥BD;
(3)因为 △AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可求解△AED的面积.
(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中,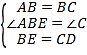 ,
,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=![]() (1+2)×2﹣
(1+2)×2﹣![]() ×2×1﹣
×2×1﹣![]() ×1×1=
×1×1=![]()


科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在班上组织的“元旦迎新晚会”中,小丽和小芳都想当节目主持人,但现在只有一个名额.小芳想出了一个用游戏来选人的办法,她将一个转盘平均分成![]() 份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.
份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.

![]() 指针指到偶数的概率是多少?指针指到奇数的概率是多少?
指针指到偶数的概率是多少?指针指到奇数的概率是多少?
![]() 这个游戏对双方公平吗?为什么?
这个游戏对双方公平吗?为什么?
![]() 若游戏不公平,请你修改转盘中的数字,使得游戏对双方公平.
若游戏不公平,请你修改转盘中的数字,使得游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
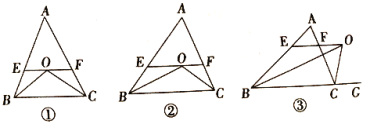
【题目】如图①,![]() 中,
中,![]() ,
,![]() 、∠C的平分线交于
、∠C的平分线交于![]() 点,过
点,过![]() 点作
点作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .试回答:
.试回答:
(1)图中等腰三角形有________个.猜想:![]() 与
与![]() 、
、![]() 之间的关系是________.说明理由;
之间的关系是________.说明理由;
(2)如图②,若![]() ,图中等腰三角形有________个,在第(1)问中
,图中等腰三角形有________个,在第(1)问中![]() 与
与![]() 、
、![]() 间的关系还存在吗?
间的关系还存在吗?
(3)如图③,若![]() 中
中![]() 的平分线
的平分线![]() 与三角形外角平分线
与三角形外角平分线![]() 交于
交于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,这时图中还有等腰三角形吗?
,这时图中还有等腰三角形吗?![]() 与
与![]() 、
、![]() 关系又如何?说明你的理由.
关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩.
(1)小明和小刚都在本周日上午去游玩的概率为 ;
(2)求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把![]() 张形状、大小相同但画面不同的风景图片全部从中间剪断,然后将四张形状相同的小图片混合在一起.现从这四张图片中随机的一次抽出
张形状、大小相同但画面不同的风景图片全部从中间剪断,然后将四张形状相同的小图片混合在一起.现从这四张图片中随机的一次抽出![]() 张.
张.
![]() 请用列表或画树状图的方法表示出上述实验所有可能结果.
请用列表或画树状图的方法表示出上述实验所有可能结果.
![]() 求这
求这![]() 张图片恰好组成一张完整风景图概率.
张图片恰好组成一张完整风景图概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com