
【题目】如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE的度数为( )
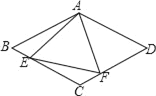
A. 30° B. 45° C. 60° D. 75°
【答案】B
【解析】首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后可求出∠AFD,∠CFE的度数.
连接AC,
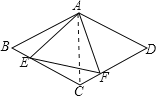
∵菱形ABCD,∴AB=BC,∠B=∠D=60°,
∴△ABC为等边三角形,∠BCD=120°
∴AB=AC,∠ACF=![]() ∠BCD=60°,
∠BCD=60°,
∴∠B=∠ACF,
∵△ABC为等边三角形,
∴∠BAC=60°,即∠BAE+∠EAC=60°,
又∠EAF=60°,即∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE与△ACF中,
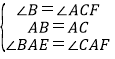 ,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AFD=180°-45°-60°=75°,
则∠CFE=180°-75°-60°=45°.
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
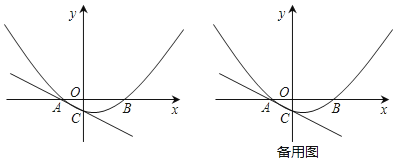
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:
(1)在离A站多少km处?
(2)判定三角形DEC的形状.
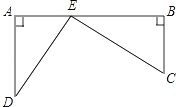
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.
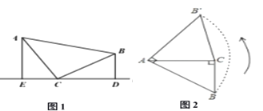
求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB,连接B,C,求△AB,C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象分别经过点(0,3),(3,0),(4,﹣5).
(1)求这个二次函数的解析式;
(2)求这个二次函数的最值;
(3)若设这个次函数图象与x轴交于点C,D(点C在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ACB时等腰三角形,求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
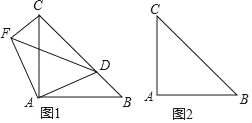
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
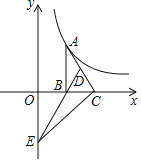
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com