
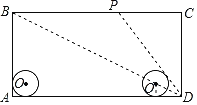
【题目】如图,在矩形ABCD中,AD=80cm,AB=40cm,半径为8cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切,此时⊙O移动了( )cm.
A.56B.72C.56或72D.不存在
【答案】B
【解析】
根据相同时间内速度的比等于路程的比,可得![]() 的值,根据相似三角形的性质,可得∠ADB=∠BDP,根据等腰三角形的判定,可得BP与DP的关系,根据勾股定理,可得DP的长,根据有理数的加法,可得P点移动的距离;根据相似三角形的性质,可得
的值,根据相似三角形的性质,可得∠ADB=∠BDP,根据等腰三角形的判定,可得BP与DP的关系,根据勾股定理,可得DP的长,根据有理数的加法,可得P点移动的距离;根据相似三角形的性质,可得![]() 的长,分类讨论:当⊙O首次到达⊙
的长,分类讨论:当⊙O首次到达⊙![]() 的位置时,当⊙O在返回途中到达⊙
的位置时,当⊙O在返回途中到达⊙![]() 位置时,根据
位置时,根据![]() 的值,可得答案.
的值,可得答案.
解:存在这种情况,
设点P移动速度为v1cm/s,⊙O2移动的速度为v2cm/s,
由题意,得![]() ,
,
如图②:

设直线OO1与AB交于E点,与CD交于F点,⊙O1与AD相切于G点,
若PD与⊙O1相切,切点为H,则O1G=O1H.
易得△DO1G≌△DO1H,
∴∠ADB=∠BDP.
∵BC∥AD,
∴∠ADB=∠CBD
∴∠BDP=∠CBD,
∴BP=DP.
设BP=xcm,则DP=xcm,PC=(80﹣x)cm,
在Rt△PCD中,由勾股定理,得
PC2+CD2=PD2,即(80﹣x)2+402=x2,
解得x=50,
此时点P移动的距离为40+50=90cm,
∵EF∥AD,
∴△BEO1∽△BAD,
∴![]() ,即
,即![]() ,
,
EO1=64cm,OO1=56cm.
①当⊙O首次到达⊙O1的位置时,⊙O移动的距离为40cm,
此时点P与⊙O移动的速度比为![]() ,
,
∵![]() ,
,
∴此时PD与⊙O1不能相切;
②当⊙O在返回途中到达⊙O1位置时,⊙O移动的距离为2(80﹣16)﹣56=72cm,
∴此时点P与⊙O移动的速度比为![]() ,
,
此时PD与⊙O1恰好相切,此时⊙O移动了72cm,
故选:B.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
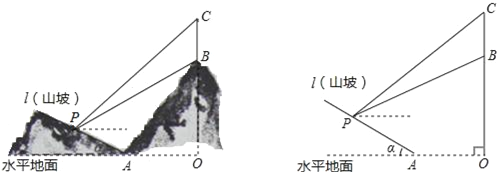
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿![]() 轴做如下移动,第一次点A向左移动3个单位长度到达点
轴做如下移动,第一次点A向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是 .
的最小值是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
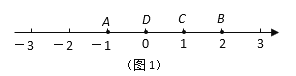
知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)数_______________________ 所表示的点是(M,N)的好点;
(2)数________________________ 所表示的点是(N,M)的好点;

(温馨提示:注意考虑M,N的左侧、右侧,不要漏掉答案)
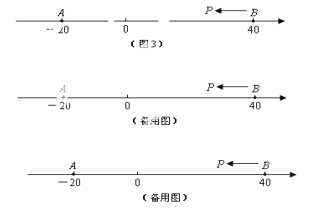
(3)如图(3)A,B为数轴上的两点,点A所表示的数为-20,点B表示的数为 40,现有一只电子蚂蚁P从点B出发,以2单位每秒的速度一直向左运动,
①当t为何值时,P是(A,B)的好点?
②当t为何值时,P是(B,A)的好点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
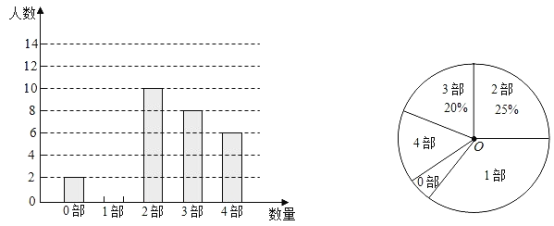
(1)请补全条形分布直方图,本次调查一共抽取了 名学生;
(2)扇形统计图中“1部”所在扇形的圆心角为 度;
(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
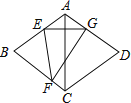
A. 6B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
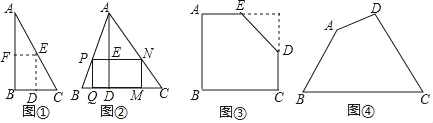
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.请画出三个图形,并直接写出其周长(所画图象全等的只算一种).
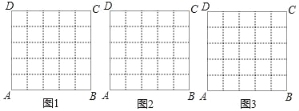
如图中所画直角三角形周长: .
如图中所画直角三角形周长: .
如图中所画直角三角形周长: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com