练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在数轴上，点A表示1，现将点A沿轴做如下移动，第一次点A向左移动3个单位长度到达点，第二次将点向右移动6个单位长度到达点，第三次将点向左移动9个单位长度到达点，按照这种移动规律移动下去，第次移动到点，如果点与原点的距离不小于20，那么的最小值是 ．

    【答案】13．

    【解析】

    试题序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，于是可得到A13表示的数为﹣17﹣3=﹣20，A12表示的数为16+3=19，则可判断点An与原点的距离不小于20时，n的最小值是13．第一次点A向左移动3个单位长度至点A1，则A1表示的数，1﹣3=﹣2﹣2；第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为﹣2+6=4；第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4﹣9=﹣5；第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为﹣5+12=7；第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7﹣15=﹣8；…；

    则A7表示的数为﹣8﹣3=﹣11，A9表示的数为﹣11﹣3=﹣14，A11表示的数为﹣14﹣3=﹣17，A13表示的数为﹣17﹣3=﹣20，A6表示的数为7+3=10，A8表示的数为10+3=13，A10表示的数为13+3=16，A12表示的数为16+3=19，

    所以点An与原点的距离不小于20，那么n的最小值是13．故答案为：13．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC．设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，连接AE、AF．那么当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

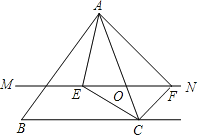
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两块完全相同的三角板Ⅰ（△ABC）和Ⅱ（△A1B1C1）如图①放置在同一平面上（∠C=∠C1=90°，∠ABC=∠A1B1C1=60°），斜边重合．若三角板Ⅱ不动，三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动，图②是滑动过程中的一个位置．

    （1）在图②中，连接BC1、B1C，求证：△A1BC1≌△AB1C；

    （2）三角板Ⅰ滑到什么位置（点B1落在AB边的什么位置）时，四边形BCB1C1是菱形？说明理由．

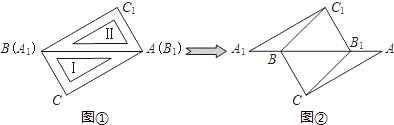
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c交x轴于A，B两点，并经过点C，已知点A的坐标是（﹣6，0），点C的坐标是（﹣8，﹣6）．

    （1）求抛物线的解析式；

    （2）求抛物线的顶点坐标及点B的坐标；

    （3）设抛物线的对称轴与x轴交于点D，连接CD，并延长CD交抛物线于点E，连接AC，AE，求△ACE的面积；

    （4）抛物线上有一个动点M，与A，B两点构成△ABM，是否存在S△ADM=S△ACD？若存在，请求出点M的坐标；若不存在，请说明理由．

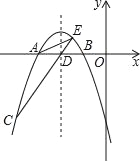
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，|a|表示a到原点的距离，这是绝对值的几何意义．进一步地，数轴上两个点A、B，分别用a、b表示，那么AB=|a－b|．（思考一下，为什么？），利用此结论，回答以下问题：

    （1）数轴上表示2和5的两点之间的距离是_____．数轴上表示－2和－5的两点之间的距离___．数轴上表示1和－3的两点之间的距离是_____；

    （2）数轴上表示x和－1的两点A、B之间的距离是___________；

    如果|AB|=2，x的值为_____；

    （3）说出|x+1|+|x+2|表示几何的意义_，该代数式的最小值是：_____；

    （4）求|x－1|+|x－2|+|x－3|+．．．+|x－2019|的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，

    以下各层均比上一层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以

    算出图1中所有圆圈的个数为1＋2＋3＋…＋n＝．

    如果图中的圆圈共有13层，请解决下列问题：

    （1）我们自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1，2，3，4，……，则最底层最左

    边这个圆圈中的数是 ；

    （2）我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数－23，－22，－21，－20，……，求

    最底层最右边圆圈内的数是_______；

    （3）求图4中所有圆圈中各数的绝对值之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线（x＜0）分别交于点C、D，且C点的坐标为（﹣1，2）．

    （1）分别求出直线AB及双曲线的解析式；

    （2）求出点D的坐标；

    （3）利用图象直接写出：当x在什么范围内取值时，y1＞y2？

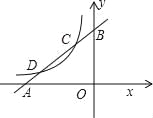
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AD＝80cm，AB＝40cm，半径为8cm的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动；⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动．已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．当⊙O到达⊙O1的位置时（此时圆心O1在矩形对角线BD上），DP与⊙O1恰好相切，此时⊙O移动了（　　）cm．

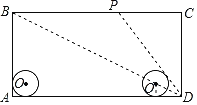
    A.56B.72C.56或72D.不存在

    查看答案和解析>>

    科目：初中数学 来源： 题型：

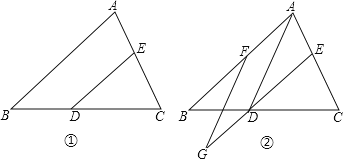
    【题目】已知：点D，E分别是△ABC的BC，AC边的中点.

    (1)如图①，若AB=10，求DE的长；

    (2)如图②,点F是AB边上的一点,FG//AD,交ED的延长线于点G.求证：AF=DG

    查看答案和解析>>

    同步练习册答案