
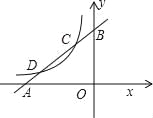
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长10cm,宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使无盖长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的侧面积(指的是高为剪去的正方形边长的长方体的侧面积)可以达到30cm2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿![]() 轴做如下移动,第一次点A向左移动3个单位长度到达点
轴做如下移动,第一次点A向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是 .
的最小值是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
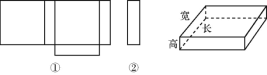
【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
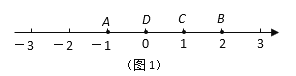
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)数_______________________ 所表示的点是(M,N)的好点;
(2)数________________________ 所表示的点是(N,M)的好点;

(温馨提示:注意考虑M,N的左侧、右侧,不要漏掉答案)
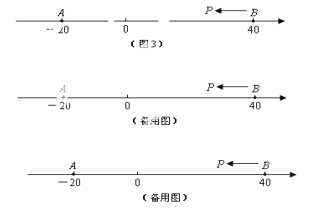
(3)如图(3)A,B为数轴上的两点,点A所表示的数为-20,点B表示的数为 40,现有一只电子蚂蚁P从点B出发,以2单位每秒的速度一直向左运动,
①当t为何值时,P是(A,B)的好点?
②当t为何值时,P是(B,A)的好点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
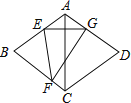
A. 6B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 完成下面的证明.
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
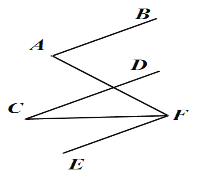
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com