
����Ŀ����ͼ����һ�ų�10cm����8cm�ij�����Ӳֽ������ܸ���ȥһ��ͬ����С�������Σ����ۺϳ�һ���ǵij�������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ���
��1��Ҫʹ�dz�������ӵĵ����Ϊ48cm2����ô��ȥ�������εı߳�Ϊ���٣�
��2������ѳ�����Ӳֽ������ֱܷ��ȥ2��ͬ����С�������κ�2��ͬ����״��ͬ����С�ij����Σ�Ȼ���ۺϳ�һ���иǵij�������ӣ���ô���IJ������ָ���Ǹ�Ϊ��ȥ�������α߳��ij�����IJ���������Դﵽ30cm2����˵�����ɣ�

���𰸡���1����ȥ�������εı߳�Ϊ1cm����2����ȥ�������α߳�Ϊ![]() cm��3cm��
cm��3cm��
��������
��1�����ȥ�������α߳�Ϊxcm�����ݳ����ε������ʽ���з��̣�10-2x����8-2x��=48����������̣��Ѳ�������Ľ���ȥ�����ɵõ�����𰸣�
��2�����ȥ�������α߳�Ϊycm���������ּ���������ͼ1����ʱ��2(8-2y)y+2��![]() y=30����ñ�������ʵ���⣻����ͼ2����ʱ���з���2(10-2y)y+2��
y=30����ñ�������ʵ���⣻����ͼ2����ʱ���з���2(10-2y)y+2��![]() y=30����˷��̣����ɵñ�С��𰸣�
y=30����˷��̣����ɵñ�С��𰸣�
�⣺��1�����ȥ�������α߳�Ϊxcm�������⣬��
��10-2x����8-2x��=48����x2-9x+8=0
���x1=8���������⣬��ȥ����x2=1��
���ȥ�������εı߳�Ϊ1cm��
��2�����IJ�������Դﵽ30cm2���������£�
���ȥ�������α߳�Ϊycm��
����ͼ1��ʾ�ķ������ۣ�
�ⷽ��2(8-2y)y+2��![]() y=30���ø÷���û��ʵ���⣮
y=30���ø÷���û��ʵ���⣮
����ͼ2��ʾ�ķ������ۣ�
�ⷽ��2(10-2y)y+2��![]() y=30��
y=30��
��y1=![]() ��y2=3��
��y2=3��
�൱��ͼ2��ʾ�ķ�����ȥ�������α߳�Ϊ![]() cm��3cmʱ����ʹ�õ����иdz�������ӵIJ�����ﵽ30 cm2��
cm��3cmʱ����ʹ�õ����иdz�������ӵIJ�����ﵽ30 cm2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A��B���㣮
![]()
��1���ֱ�д��A��B�����ʾ�������� ������ ����
��2������C��ʾ��0.5���ѵ�C��ʾ����ͼ��ʾ�������ϣ�
��3������B�����ƶ�3����λ���ȣ��õ���D����A��B��C��D����ʾ���ĸ��������������ӵĽ������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
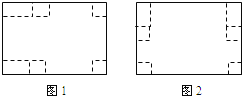
����Ŀ����ͼ����������ABCD�У���P��AB���ϣ�AE��DP��E�㣬CF��DP��F�㣬��AE��5��CF��9����EF��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ��ͬ�����ǰ����ABC���͢���A1B1C1����ͼ�ٷ�����ͬһƽ���ϣ���C=��C1=90������ABC=��A1B1C1=60������б���غϣ������ǰ�������ǰ�������ǰ�����ڵ�ƽ�������һ�����ͼ���ǻ��������е�һ��λ�ã�
��1����ͼ���У�����BC1��B1C����֤����A1BC1�ա�AB1C��
��2�����ǰ��ʲôλ�ã���B1����AB�ߵ�ʲôλ�ã�ʱ���ı���BCB1C1�����Σ�˵�����ɣ�
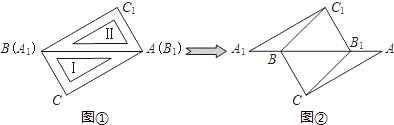
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�۲�һ����a1��3��a2��32��a3��33��a4��34���������ִӵڶ��ʼ��ÿһ����ǰһ��֮����һ�����������������_______�����ݴ˹��ɣ����an��nΪ����������ʾ������еĵ�n���ôa6��_______��an��_______���������ݵ���ʽ��ʾ��
(2)�����Ҫ��l��2��22��23����������210��ֵ������S10��l��2��22��23����������210��,����ʽ����ͬ����2����_______�ڣ��ɢڼ�ȥ��ʽ����S10��_______��
(3)��(1)�����й���20���S20��3��32��33��34������320���������������ɺͷ�������S20��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��![]() x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
��1���������ߵĽ���ʽ��
��2���������ߵĶ������꼰��B�����ꣻ
��3���������ߵĶԳ�����x�ύ�ڵ�D������CD�����ӳ�CD���������ڵ�E������AC��AE������ACE�������
��4������������һ������M����A��B���㹹����ABM���Ƿ����S��ADM=![]() S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
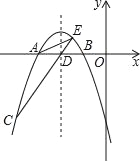
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����|a|��ʾa��ԭ��ľ��룬���Ǿ���ֵ�ļ������壮��һ���أ�������������A��B���ֱ���a��b��ʾ����ôAB=|a��b|����˼��һ�£�Ϊʲô���������ô˽��ۣ��ش��������⣺
��1�������ϱ�ʾ2��5������֮��ľ�����_____�������ϱ�ʾ��2�ͣ�5������֮��ľ���___�������ϱ�ʾ1�ͣ�3������֮��ľ�����_____��
��2�������ϱ�ʾx�ͣ�1������A��B֮��ľ�����___________��
���|AB|=2��x��ֵΪ_____��
��3��˵��|x+1|+|x+2|��ʾ���ε�����_���ô���ʽ����Сֵ�ǣ�_____��
��4����|x��1|+|x��2|+|x��3|+������+|x��2019|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ��ڵ�A��B����˫����![]() ��x��0���ֱ��ڵ�C��D����C�������Ϊ����1��2����
��x��0���ֱ��ڵ�C��D����C�������Ϊ����1��2����
��1���ֱ����ֱ��AB��˫���ߵĽ���ʽ��
��2�������D�����ꣻ
��3������ͼ��ֱ��д������x��ʲô��Χ��ȡֵʱ��y1��y2��
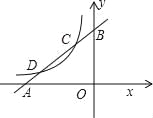
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a�����ĸ�������b����С������������c��a+b����ش��������⣺
![]()
��1����ֱ��д��a��b��c��ֵ��a���� ����b���� ����c���� ����
��2��a��b��c������������Ӧ�ĵ�ֱ�ΪA��B��C��������ͼ�������ϱ�ʾ��A��B��C���㣻
��3���ڣ�2��������£���A��B��C��ʼ���������˶�������A����C��ÿ��1����λ���ٶ������˶���ͬʱ����B��ÿ��5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�AB��BC��ֵ�Ƿ�����ʱ��ı仯���ı䣿���仯����˵�����ɣ������䣬�����AB��BC��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com