
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.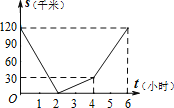 B.
B.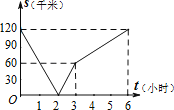
C.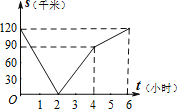 D.
D.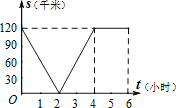
【答案】B
【解析】
根据题意求出2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,进而根据相遇前、相遇后两个阶段得出相应的分段函数,从而找出符合题意的图象.
解:根据题意,两人同时相向出发,甲到达B地时间为:![]() =6小时,乙到达A地:
=6小时,乙到达A地:![]() =3小时.
=3小时.
根据题意,分成两个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地;
相遇前,s=120﹣(20+40)t=120﹣60t(0≤t≤2),当两者相遇时,t=2,s=0,
相遇后,当乙到达A地前,甲乙均在行驶,即s=(20+40)(t﹣2)=60t﹣120(2≤t≤3),当乙到达A地时,此时两者相距60千米;
当乙到达A地后,剩下甲在行驶,即s=60+20(t﹣3)=20t(3≤t≤6),
故: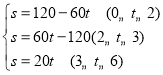
故选B.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
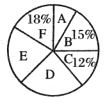
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数 y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方,所得的折线是函数y=![]() (b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
(b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
A.-5≤b≤-1B.-3≤b≤-1C.-2≤b≤0D.-3≤b≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费每户每月用水量如果未超过20t,按每吨2.5元收费.如果超过20t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为xt,应收水费为y元.
(1)分别写出每月用水量未超过20t和超过20t时y与x间的关系式.
(2)若该城市某户4月份水费平均为每吨2.8元,求该户4月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com