
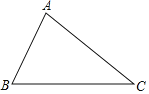
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
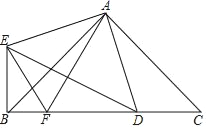
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,给出如下定义:对于点P(m,n),若点Q(2﹣m,n﹣1),则称点Q为点P的“δ点”.例如:点(﹣2,5)的“δ点”坐标为(4,4).
(1)某点的“δ点”的坐标是(﹣1,3),则这个点的坐标为 ;
(2)若点A的坐标是(2﹣m,n﹣1),点A的“δ点”为A1点,点A1的“δ点”为A2点,点A2的“δ点”为A3点,…,点A1的坐标是 ;点A2015的坐标是 ;
(3)函数y=﹣x2+2x(x≤1)的图象为G,图象G上所有点的“δ点”构成图象H,图象G与图象H的组合图形记为“图形Ю”,当点(p,q)在“图形Ю”上移动时,若k≤p≤1+2![]() ,﹣8≤q≤1,求k的取值范围
,﹣8≤q≤1,求k的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
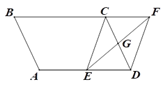
A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.
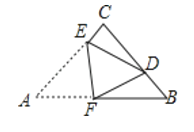
【答案】![]()
【解析】分析:过点D作DG![]() AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得![]() ,所以DB=
,所以DB=![]() ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得![]() ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得![]() ,
, ![]() ;
;
设AF=DF=x,则FG= ![]() ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程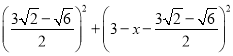 =
=![]() ,解得
,解得![]() ,从而求得
,从而求得![]() .的值
.的值
详解:
如图所示,过点D作DG![]() AB于点G.
AB于点G.
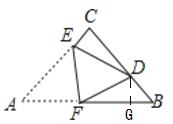
根据折叠性质,可知△AEF![]() △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得![]() ,
,
∴DB=![]() ;
;
在Rt△ABC中,由勾股定理得![]() ;
;
在Rt△DGB中, ![]() ,
, ![]() ;
;
设AF=DF=x,得FG=AB-AF-GB=![]() ,
,
在Rt△DFG中, ![]() ,
,
即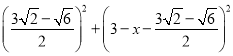 =
=![]() ,
,
解得![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案为: ![]() .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.
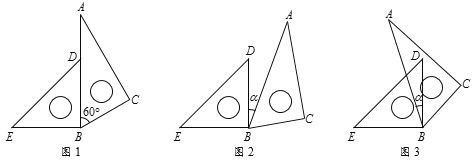
(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.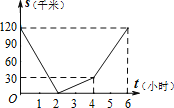 B.
B.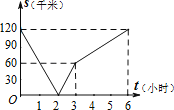
C.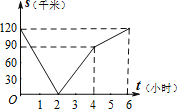 D.
D.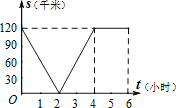
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com