
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.
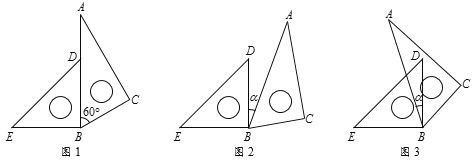
(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
【答案】(1)150°;(2)20°;(3)32°;(4)30°.
【解析】
(1)根据角的和差即可得出结论;
(2)根据角的和差即可得出结论;
(3)根据角的和差即可得出结论.
(1)∵∠EBC=∠EBD+∠ABC,
∴∠EBC=90°+60°=150°.
(2)∵∠EBC=∠EBD+∠DBA+∠ABC,
∴∠α=∠EBC-∠EBD-∠ABC=170°-90°-60°=20°;
(3)∵∠EBC=∠EBD+∠DBC=∠EBD+∠ABC-∠α,
∴∠α=∠EBD+∠ABC-∠EBC=90°+60°-118°=32°;
(4)∵∠ABE=∠DBE-∠α=90°-∠α,∠DBC=∠ABC-∠α=60°-∠α,
∴∠ABE-∠DBC=(90°-∠α)-(60°-∠α)=90°-∠α-60°+∠α=30°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 的路线以
的路线以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
![]()
(1)当![]() 时,则线段
时,则线段![]()
![]() ,线段
,线段![]()
![]() .
.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 的中点为
的中点为![]() ,问
,问![]() 的长是否变化?与点
的长是否变化?与点![]() 的位置是否无关?
的位置是否无关?
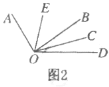
(4)知识迁移:如图2,已知![]() ,过角的内部任一点
,过角的内部任一点![]() 画射线
画射线![]() ,若
,若![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,问∠EOC的度数是否变化?与射线
,问∠EOC的度数是否变化?与射线![]() 的位置是否无关?
的位置是否无关?
查看答案和解析>>
科目:初中数学 来源: 题型:
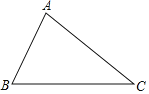
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 平分
平分![]() ,设
,设![]() .
.
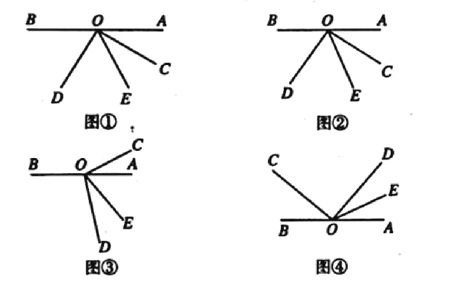
(1)如图①所示,若![]() ,则
,则![]() .
.
(2)若将![]() 绕点
绕点![]() 旋转至图②的位置,试用含
旋转至图②的位置,试用含![]() 的代数式表示
的代数式表示![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若将![]() 绕点
绕点![]() 旋转至图③的位置,则用含
旋转至图③的位置,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
(4)若将![]() 绕点
绕点![]() 旋转至图④的位置,继续探究
旋转至图④的位置,继续探究![]() 和
和![]() 的数量关系,则用含
的数量关系,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
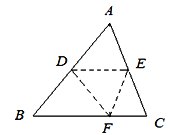
①△BDF是等腰三角形;
②DE=![]() BC;
BC;
③四边形ADFE是菱形;
④∠BDF+∠FEC=2∠A.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
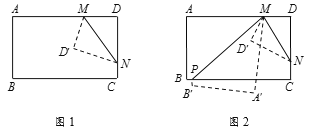
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
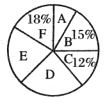
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com