
【题目】已知:点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 平分
平分![]() ,设
,设![]() .
.
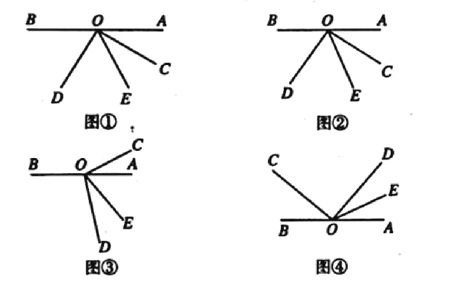
(1)如图①所示,若![]() ,则
,则![]() .
.
(2)若将![]() 绕点
绕点![]() 旋转至图②的位置,试用含
旋转至图②的位置,试用含![]() 的代数式表示
的代数式表示![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若将![]() 绕点
绕点![]() 旋转至图③的位置,则用含
旋转至图③的位置,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
(4)若将![]() 绕点
绕点![]() 旋转至图④的位置,继续探究
旋转至图④的位置,继续探究![]() 和
和![]() 的数量关系,则用含
的数量关系,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
【答案】(1)50;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据“∠COD=90°,∠COE=25°”求出∠DOE的度数,再结合角平分线求出∠AOD的度数,即可得出答案;
(2)重复(1)中步骤,将∠COE的度数代替成![]() 计算即可得出答案;
计算即可得出答案;
(3)根据图得出∠DOE=∠COD-∠COE=90°-![]() ,结合角平分线的性质以及平角的性质计算即可得出答案;
,结合角平分线的性质以及平角的性质计算即可得出答案;
(4)根据图得出∠DOE=∠COE-∠COD=![]() -90°,结合角平分线的性质以及平角的性质计算即可得出答案.
-90°,结合角平分线的性质以及平角的性质计算即可得出答案.
解:(1)∵∠COD=90°,∠COE=25°
∴∠DOE=∠COD-∠COE=65°
又OE平分∠AOD
∴∠AOD=2∠DOE=130°
∴∠BOD=180°-∠AOD=50°
(2)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COD-∠COE=90°-![]()
又OE平分∠AOD
∴∠AOD=2∠DOE=180°-![]()
∴∠BOD=180°-∠AOD=2![]()
(3)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COD-∠COE=90°-![]()
又OE平分∠AOD
∴∠AOD=2∠DOE=180°-![]()
∴∠BOD=180°-∠AOD=2![]()
(4)∵∠COD=90°,∠COE=![]()
∴∠DOE=∠COE-∠COD=![]() -90°
-90°
又OE平分∠AOD
∴∠AOD=2∠DOE=![]() -180°
-180°
∴∠BOD=180°-∠AOD=360°-2![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
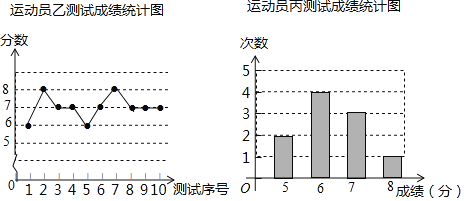
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
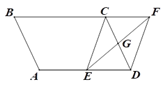
A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A.B两种型号车的进货和销售价格如表,问应如何进货才能使这批车获利最多?
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.
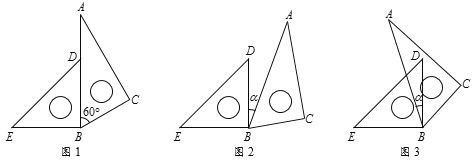
(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
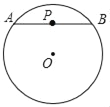
【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=![]() x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com