
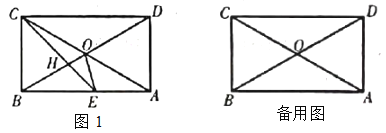
【题目】如图,矩形![]() 中,
中,![]() ,对角线
,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的平分线
的平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() .
.
(l)求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)求![]() .
.
【答案】(1)75°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由矩形的性质可得AB∥CD,AO=CO=BO=DO,由角平分线的性质和平行线的性质可求BC=BE=BO,即可求解;
(2)过点H作FH⊥BC于F,由直角三角形的性质可得FH=![]() BF,BC=
BF,BC=![]() BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
(3)过点C作CN⊥BO于N,由直角三角形的性质可求BC=![]() BF+BF=BO=BE,OH=OB-BH=
BF+BF=BO=BE,OH=OB-BH=![]() BF-BF,CN=
BF-BF,CN=![]() BC=
BC=![]() BF,即可求解.
BF,即可求解.
解:(1)∵四边形ABCD是矩形
∴AB∥CD,AO=CO=BO=DO,
∴∠DCE=∠BEC,
∵CE平分∠BCD
∴∠BCE=∠DCE=45°,
∴∠BCE=∠BEC=45°
∴BE=BC
∵∠BAC=30°,AO=BO=CO
∴∠BOC=60°,∠OBA=30°
∵∠BOC=60°,BO=CO
∴△BOC是等边三角形
∴BC=BO=BE,且∠OBA=30°
∴∠BOE=75°
(2)如图,过点H作FH⊥BC于F,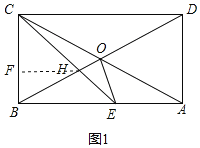
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=1
BF+BF=1
∴BF=![]() ,
,
∴FH=![]() ,
,
∴S△BCH=![]() ×BC×FH=
×BC×FH=![]() ;
;
(3)如图,过点C作CN⊥BO于N,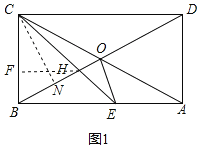
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=BO=BE,
BF+BF=BO=BE,
∴OH=OB-BH=![]() BF-BF
BF-BF
∵∠CBN=60°,CN⊥BO
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 平分
平分![]() ,设
,设![]() .
.
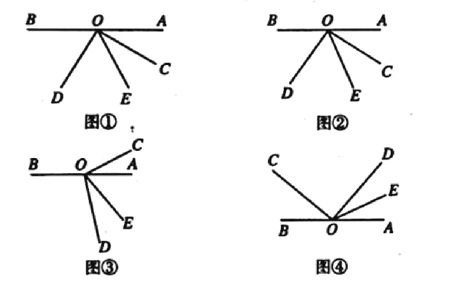
(1)如图①所示,若![]() ,则
,则![]() .
.
(2)若将![]() 绕点
绕点![]() 旋转至图②的位置,试用含
旋转至图②的位置,试用含![]() 的代数式表示
的代数式表示![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若将![]() 绕点
绕点![]() 旋转至图③的位置,则用含
旋转至图③的位置,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
(4)若将![]() 绕点
绕点![]() 旋转至图④的位置,继续探究
旋转至图④的位置,继续探究![]() 和
和![]() 的数量关系,则用含
的数量关系,则用含![]() 的代数式表示
的代数式表示![]() 的大小,即
的大小,即![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
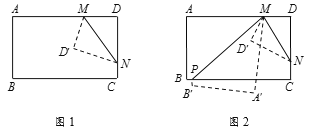
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
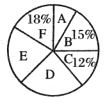
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费每户每月用水量如果未超过20t,按每吨2.5元收费.如果超过20t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为xt,应收水费为y元.
(1)分别写出每月用水量未超过20t和超过20t时y与x间的关系式.
(2)若该城市某户4月份水费平均为每吨2.8元,求该户4月份用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com