
Àƒäãá¢À¢çÌú·òúééú·åùÑ₤çáØ£üŸøÄ؈¥¥ò¾ÈÛüôêÅë¥ÝÚøÅçáò»ƒïñøÝÞòú¥æÀÂØØÀÂáÖ໡—åùÑ₤åÝòÛÇöçÌú·ýãòåçá°è¥´È˜¿Ìå·öˆû¢Çöýãòåê˜Å½çÌú·10¡—Șû¢çÌú·ç§ö£1¡—¥ú1ñøÈÛ
ýãòåÅ·¤é | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
°è¥´È´ñøÈˋ | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
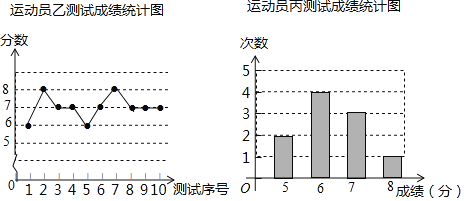
È´1ÈˋÅÇ°—åùÑ₤åÝ¥æýãòå°è¥´çáøÖò»¤ëøÅö£ò»È£
È´2ÈˋòåÇÆ󧃪ò»¤ëñ§ýŸê§¡—§úÑàæܤüñøö—Șà¶åÖù«ûúà»àùøÅîÀåþØ£ö£çÌú·°è¥´ÆéÅÐúاüöˆöàÑ´çá§Æú·áÉòøæ¼öˆæåÆèàùȘáÐàüöˆîÀùÙ¡■¤üòòȢȴýö¢¥ò»ƒïȤà»àù°è¥´çáñ§ýŸñøÝÞöˆS¥æ2ȧ0.8ÀÂSØØ2ȧ0.4ÀÂsÝ«2ȧ0.81Èˋ
ÀƒÇÞ¯¡À¢(1) ¥æçáøÖò»¤ëøÅö£ò»Ñ¥òú7ñø;(2) îÀØØåùÑ₤åÝ¡■¤üòò,âÚÆ襫§ãö—
Àƒ§ãö—À¢
È´1Èˋ¿ÜýšÝÚ¡þ¢èøˆ¥æåùÑ₤åÝýãòå°è¥´çáøÖò»¤ëøÅö£ò»Ñ¥òú7ñøÈ£
È´2ÈˋñøÝÞúµçûò»ƒïçá󧃪ò»È˜à£¤µ§Ã¤üñ§ýŸæ¼°—éÅÑü¥Ç¢èÈÛ
È´1Èˋ¥æåùÑ₤åÝýãòå°è¥´øÅ7°—üøçáÇöò»æŸÑÁȘ¿òøÖò»öˆ7È£
°è¥´ééÅ·öˆÈ¤5Ș6Ș7Ș7Ș7Ș7Ș7Ș8Ș8Ș8Ș
ùªØå¥æçáøÅö£ò»öˆ![]() ȧ7Ș
ȧ7Ș
ùªØå¥æçáøÖò»¤ëøÅö£ò»Ñ¥òú7ñøÈÛ
È´2ÈˋÀÔ![]() ȧ
ȧ![]() È´7+6+8+7+7+5+8+7+8+7Èˋȧ7È´ñøÈˋȘ
È´7+6+8+7+7+5+8+7+8+7Èˋȧ7È´ñøÈˋȘ
![]() ȧ
ȧ![]() È´6+6+7+7+7+7+7+7+8+8Èˋȧ7È´ñøÈˋȘ
È´6+6+7+7+7+7+7+7+8+8Èˋȧ7È´ñøÈˋȘ
![]() ȧ
ȧ![]() È´5Àê2+6Àê4+7Àê3+8Àê1Èˋȧ6.3È´ñøÈˋȘ
È´5Àê2+6Àê4+7Àê3+8Àê1Èˋȧ6.3È´ñøÈˋȘ
ÀÁ![]() ȧ
ȧ![]() ȘS¥æ2ȃSØØ2Ș
ȘS¥æ2ȃSØØ2Ș
ÀÁîÀØØåùÑ₤åÝ¡■¤üòòÈÛ


 ¢ˆÅáêñü¯¢ö¢öêñÆŠçË別šýãüçêÅÇÞ¯¡
¢ˆÅáêñü¯¢ö¢öêñÆŠçË別šýãüçêÅÇÞ¯¡ ¢ˆÅáòåƒÚóÖáˋ°ÍÇä100ñøüçêÅÇÞ¯¡
¢ˆÅáòåƒÚóÖáˋ°ÍÇä100ñøüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢À¯úÅò祾úÃîÏ躢öØ硤çÈÀÝòúöØòÅæ¼Øç¡á¡ÿçáØ£üŸøÄ؈ƒìÇŠÈÛá°øÅîÏöˆêù§ã݃ÅÈîÏèºó§ƒªû¢äšçá¢öëãîÏü¯òÝ¥ðúÕ¢—ȘùÌ£º°ÕàÀý¢ñøîÏ躧½ÅÅöòƒÚç¼ýÕȘý§¨ç¼ýէÿ«ñøöˆ AȘBȘCȘD ùá¡—çà¥Ñ.èÒîÏü¯òÝ¥ðöˆtÈ´ÅÀòÝÈˋȘA:tÈ¥1ȘB:1ÀÉtÈ¥1.5ȘC:1.5ÀÉtÈ¥2ȘD:tÀï2 Ș¡ªƒïç¼ýէÿ«£ÌøóêùàÓë¥ùªòƒçáê§ñªý£ëõí«çáë°¥óë¥ÈÛúŠáСªƒïë¥øÅÅéü§ãÇÞüôêÅöòäãȤ
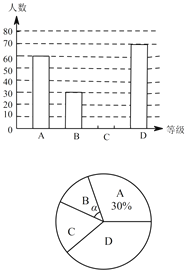
È´1Èˋ¡ûÅÈ¿ýç¼ýÕêùÑÁèìû«îÏèºÈ£
È´2Èˋ§¨ä¾Åöë°¥óë¥ý¿°ðëõí«È£
È´3Èˋúµ°—ÝÚòƒ Bçà¥ÑçáèàÅöåýÅá§ú Îê çáÑàò»È£
È´4ÈˋåÖÇùÇööòƒÚç¼ýÕøÅȘ¥æ¯ÁÆÅ 2 àù󧃪û¢äš¢öëãîÏü¯òݥ𰘿» 2 ÅÀòÝȘØدÁÆÅ 3 àù󧃪û¢äš¢öëãîÏü¯òݥ𰘿» 2 ÅÀòÝȘà¶ÇÆíã 5 àùøÅàöîÀ 2àùàËýö¥Ææªä¡È˜òåÆûêÅÝÚ£·£Ùò¼æÇë¥çáñ§ñ´úµîÀ°—çá2àù
âÇæåý£ë˜¯Á¥Ñçá¡éôòÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
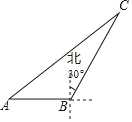
Àƒäãá¢À¢àÓë¥È˜¤ÈøÅØ£ÆÌǘåÖAÇÎÆŠÅÀç¤CüÁƒÁ70¤ÈâÿȘඡûÆÌǘÆèö¼ü·Ñ¨¤§ÅÅ30¤Èâÿç§ÇÿBÇÎȘÇùòÝýãçûÅÀç¤Cö£ÆÖBçáÝÝó¨Ñ¨30ÀÐñ§ü·èüȘ巡ûÆÌǘÇùòÝÆŠÅÀç¤CøÛ¥ðçáƒÁâŠòú_____¤ÈâÿÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢á°üŸ¿Ê°äÆè¥æÀÂØØꧡ—¿Ê°äÑƤüæ¼ëõ°èȘüàÆè¥æÑÆçËÑâæ—3äšÈ˜òÈüôçá¿Êæ¼Æè¥æÀÂØØ꧿ʰäÑƤüæ¼ëõ°èȘ¿Ê°ä§½ÑàôºæÐàÓë¥ùªòƒçá¤₤ò»¿ÄüçȤ
È´1Èˋúµ°—ë¥üµøÅÂÖý¢ñøçá§ãö—ò§È˜ýÂúµ°—ëõ°èÇùüŸ¿Ê°ä¿ýÅÒçáäšò»È£
È´2Èˋ¡û¿Ê°ä¿ýøÏ¡Ñ8ë·åˆÈ˜à¶¯Çëõ°èçá¿Êæ¼ê¢ùªí¥Ýàâ»øÏ¡Ñ¿ÊæòȘ¥æ¿Ê°äÑÆÆÎçûÑÁèìåˆÈ¢
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜çÐEÀÂFñøÝÞòúêãÅöABCDçáÝÔBCÀÂCDèüçáçÐȘúØÀüEAF=ÀüD=60ÀÐȘÀüFAD=45ÀÐȘå·ÀüCFE=_____ÑàÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
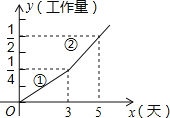
Àƒäãá¢À¢á°òÅöÍåôåãÆ—êù°øŽú¢§çÆõȘ嚰èý¢ñøçÄú½¤Õâååø¤ÎȘᰯÛÅáæÕø₤§¶¥Ý°ÿ¥₤êùý¢ñøæò§ÞȘ¥ó£Û¿¤ô·¥æÀÂØØê§øøƒàåøöÿóñ¿ý4000¥±ùëëªåøú½È˜Øîøˆû¢¥±¥æøøöÿóñçá¥Ü¡þÝàû¢¥±ØØøøöÿóñçá¥Ü¡þ¿µ10åˆÈ˜Æû300刿¤ô·¥æøøöÿóñçᥱò»úÀ¤ûÆŠÆû240刿¤ô·ØØøøöÿóñçᥱò»üÁë˜.
È´1Èˋúµ¥æÀÂØØê§øøƒàåøöÿóñû¢¥±çá¥Ü¡þ¡¼òúÑÁèìåˆÈ¢
È´2ÈˋƒÙç¼ýÕȘåøú½ÑåØØøøöÿóñ¥±ò»çáÅÒúµê¢òú¥æøøöÿóñ¥±ò»çá3ÝÑȘඡû¯ÛÅáæÕø₤¯ÇííÇùÅÒúµçáÝà⻿¤ô·íã4000¥±öÿóñȘÅÒ°ÿ¥₤æò§ÞÑÁèìåˆÈ¢
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥1Ș![]() òúüÔÑö
òúüÔÑö![]() èüØ£Ñ₤çÐȘîÄ
èüØ£Ñ₤çÐȘîÄ![]() çáôñüÔØå
çáôñüÔØå![]() çáùìÑàëªñçåùÑ₤1ÇöȘ
çáùìÑàëªñçåùÑ₤1ÇöȘ![]() òúüÔÑö
òúüÔÑö![]() çáøÅçÐȘ
çáøÅçÐȘ![]() ȘèÒçÐ
ȘèÒçÐ![]() çáåùÑ₤òÝ¥ðöˆ
çáåùÑ₤òÝ¥ðöˆ![]() .
.
![]()
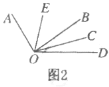
È´1ÈˋçÝ![]() òÝȘå·üÔÑö
òÝȘå·üÔÑö![]()
![]() ȘüÔÑö
ȘüÔÑö![]()
![]() .
.
È´2ÈˋÆû¤˜![]() çáǺò»ò§ÝÚòƒåùÑ₤¿»°äøÅ
çáǺò»ò§ÝÚòƒåùÑ₤¿»°äøÅ![]() çá°Ê.
çá°Ê.
È´3ÈˋåÖåùÑ₤¿»°äøÅȘà¶![]() çáøÅçÐöˆ
çáøÅçÐöˆ![]() Șöò
Șöò![]() çá°ÊòúñþÝð£₤ȢƊçÐ
çá°ÊòúñþÝð£₤ȢƊçÐ![]() çáö£øûòúñþöß¿ÄÈ¢
çáö£øûòúñþöß¿ÄÈ¢
È´4ÈˋøˆòÑú´ØóȤàÓë¥2ȘØîøˆ![]() Ș¿»§úçááÖý¢àöØ£çÐ
Ș¿»§úçááÖý¢àöØ£çÐ![]() £ÙèðüÔ
£ÙèðüÔ![]() Șà¶
Șà¶![]() ÀÂ
ÀÂ![]() ñøÝÞó§ñø
ñøÝÞó§ñø![]() ¤ë
¤ë![]() ȘöòÀüEOCçáÑàò»òúñþÝð£₤ȢƊèðüÔ
ȘöòÀüEOCçáÑàò»òúñþÝð£₤ȢƊèðüÔ![]() çáö£øûòúñþöß¿ÄÈ¢
çáö£øûòúñþöß¿ÄÈ¢
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜øÝüÔy=ˋ![]() x+cÆŠxøç£ÆÖçÐAÈ´3Ș0ÈˋȘƊyøç£ÆÖçÐBȘéæöÿüÔy=ˋ
x+cÆŠxøç£ÆÖçÐAÈ´3Ș0ÈˋȘƊyøç£ÆÖçÐBȘéæöÿüÔy=ˋ![]() x2+bx+cƒÙ¿»çÐAȘBÈÛ
x2+bx+cƒÙ¿»çÐAȘBÈÛ
È´1ÈˋúµçÐBçáæ½Ýõ¤ëéæöÿüÔçá§ãö—ò§È£
È´2ÈˋMÈ´mȘ0ÈˋöˆxøÃèüØ£Ñ₤çÐȘ¿»çÐMúØÇ¿øÝÆÖxøÃçáøÝüÔÆŠøÝüÔAB¥¯éæöÿüÔñøÝÞ§£ÆÖçÐPȘNÈÛ
ÂìçÐMåÖüÔÑöOAèüåùÑ₤Șà¶ØåBȘPȘNöˆÑËçÐçá໧úÅöÆŠÀ¼APMüÁùóȘúµçÐMçáæ½ÝõÈ£
ÂÖçÐMåÖxøÃèüæåÆèåùÑ₤Șà¶à»¡—çÐMȘPȘNøÅúÀÆÅØ£çÐòúóðù■ê§çÐùªê˜üÔÑöçáøÅçÐÈ´à»çÐøĤü°»ëãÈˋȘ巰óMȘPȘNà»çÐöˆÀ¯¿ýÅ°çÐÀÝÈÛúŠøݧÆÅÇ°—ò¿çûMȘPȘNà»çаèöˆÀ¯¿ýÅ°çÐÀÝçámçáøçÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢ØîøˆÈ¤çÐ![]() öˆøÝüÔ
öˆøÝüÔ![]() èüØ£çÐȘ
èüØ£çÐȘ![]() ȘèðüÔ
ȘèðüÔ![]() ó§ñø
ó§ñø![]() ȘèÒ
ȘèÒ![]() ÈÛ
ÈÛ
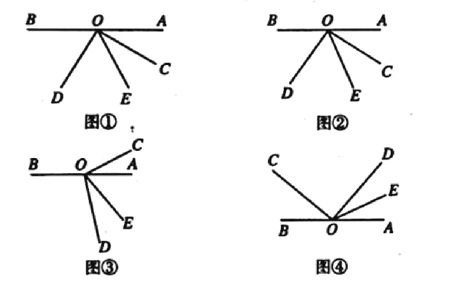
È´1ÈˋàÓë¥ÂìùªòƒÈ˜à¶![]() Șå·
Șå·![]() ÀÀÀÀÀÀÀÀ ÈÛ
ÀÀÀÀÀÀÀÀ ÈÛ
È´2Èˋට¨![]() àóçÐ
àóçÐ![]() Å»æˆøêë¥ÂÖçáö£øûȘòåÆû¤˜
Å»æˆøêë¥ÂÖçáö£øûȘòåÆû¤˜![]() çáǺò»ò§ÝÚòƒ
çáǺò»ò§ÝÚòƒ![]() çáǵÅÀȘýÂùçû¼âÚÆèÈ£
çáǵÅÀȘýÂùçû¼âÚÆèÈ£
È´3Èˋට¨![]() àóçÐ
àóçÐ![]() Å»æˆøêë¥ÂÜçáö£øûȘå·Æû¤˜
Å»æˆøêë¥ÂÜçáö£øûȘå·Æû¤˜![]() çáǺò»ò§ÝÚòƒ
çáǺò»ò§ÝÚòƒ![]() çáǵÅÀȘ¥Ç
çáǵÅÀȘ¥Ç![]() ÀÀÀÀÀÀÀÀÈÛ
ÀÀÀÀÀÀÀÀÈÛ
È´4Èˋට¨![]() àóçÐ
àóçÐ![]() Å»æˆøêë¥ÂÉçáö£øûȘ¥äŽ䧃¢
Å»æˆøêë¥ÂÉçáö£øûȘ¥äŽ䧃¢![]() ¤ë
¤ë![]() çáò»ê¢¿ÄüçȘå·Æû¤˜
çáò»ê¢¿ÄüçȘå·Æû¤˜![]() çáǺò»ò§ÝÚòƒ
çáǺò»ò§ÝÚòƒ![]() çáǵÅÀȘ¥Ç
çáǵÅÀȘ¥Ç![]() ÀÀÀÀÀÀÀÀ ÈÛ
ÀÀÀÀÀÀÀÀ ÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¿º¥òîÏÅÈÆéîÀ - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com