
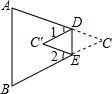
 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°. 分析 先根据三角形的内角和定理求出∠CEF+∠CFE=∠A+∠B,再根据折叠变换的性质,即可求出∠CEC′+∠CEC′的度数,然后利用两个平角的度数求解即可.
解答 解:如图,∵∠CEF+∠CFE+∠C=∠A+∠B+∠C,
∴∠CEF+∠CFE=∠A+∠B=75°+65°=140°,
又将纸片的一角折叠,使点C落在△ABC内,
∴∠C′EF+∠C′F=∠CEF+∠CFE=140°,
∴∠CEC′+∠CEC′=140°+140°=280°,
∵∠1=40°,
∴∠2=180°×2-∠CEC′+∠CEC′-∠1=360°-280°-40°=40°.
故答案为:40°.
点评 本题考查了三角形的内角和定理,翻折变换的性质,熟练掌握翻折变换的性质是解题的关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨(元) | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 作两边的中垂线的交点 | B. | 作两边上的高线的交点 | ||
| C. | 作两边上的中线的交点 | D. | 作两角平分线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-25}$=-5 | B. | -$\sqrt{3.6}$=-0.6 | C. | $\sqrt{(-13)^{2}}$=13 | D. | $\sqrt{36}$=±6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 用长为8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是$\frac{8}{3}$m2(铝合金条遮光部分忽略不计).
用长为8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是$\frac{8}{3}$m2(铝合金条遮光部分忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com