
分析 根据题意可以求出a1,a2,a3,a4的值,然后观察规律即可解答本题.
解答 解:由题目可得,a1=-3,
${a}_{2}=\frac{1}{1-{a}_{1}}=\frac{1}{1-(-3)}=\frac{1}{4}$,
${a}_{3}=\frac{1}{1-{a}_{2}}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}$,
${a}_{4}=\frac{1}{1-{a}_{3}}=\frac{1}{1-\frac{4}{3}}=-3$,
由上可知,三个为一组,2015÷3=671…2,
故${a}_{2015}=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查根据数字的变化找寻其中的变化规律,关键是先列出这组数据的几个,观察变化规律,找出几个数据为一组,从而推导出所求的数据是多少.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (x+3)2=$\frac{1}{3}$ | B. | (x+$\frac{3}{4}$)2=$\frac{1}{2}$ | C. | (3x+1)2=1 | D. | (x+$\frac{3}{4}$)2=$\frac{17}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
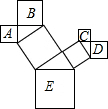 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com