
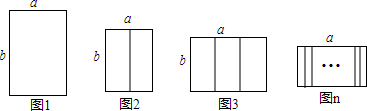
分析 (1)根据长度为1,可得出a与b的关系式,然后可表示出图1的面积,利用正方形面积最大求出即可;
(2)根据长度为1,可得出a与b的关系式,然后可表示出图2的面积,利用配方法求最值即可;
(3)利用(2)中所求方法即可得出答案.
解答 解:根据题意:①中有2(a+b)=1,且s=ab的最大值当且仅当矩形为正方形时,即a=b时所围成的矩形框面积最大,即$\frac{a}{b}$=1.
故答案为:1;
②有2个a,有3个b,则2a+3b=1,故b=$\frac{1-2a}{3}$,当且仅当矩形为正方形时,s=ab=$\frac{-2{a}^{2}+a}{3}$=-$\frac{2}{3}$(a-$\frac{1}{4}$)2+$\frac{1}{24}$,
则b=$\frac{1}{6}$,故$\frac{a}{b}$=$\frac{\frac{1}{4}}{\frac{1}{6}}$=$\frac{3}{2}$时S取得最大值.
故答案为:$\frac{3}{2}$;
③如图,有2个a,有(n+1)个b,故当且仅当矩形为正方形时,即(n+1)b=2a时,s=ab取得最大值,即$\frac{a}{b}$=$\frac{n+1}{2}$.
故答案为:$\frac{n+1}{2}$.
点评 本题考查了二次函数的应用,解答本题的关键是根据铁丝长度为1得出a与b的关系式,注意掌握配方法求函数的最值,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,AD是△ABC的角平分线,AE⊥BC于点E,若∠BAC=108°,∠C=56°,则∠DAE的度数是( )
如图所示,AD是△ABC的角平分线,AE⊥BC于点E,若∠BAC=108°,∠C=56°,则∠DAE的度数是( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com