
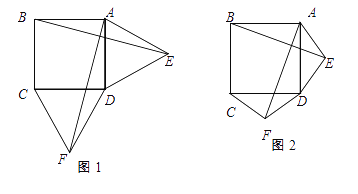
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
【答案】(Ⅰ)AF=BE,AF⊥BE. (Ⅱ)结论成立.
【解析】试题分析:(1)根据SAS易证△ADE≌△DCF,即可证明AF与BE的数量关系是AF=BE,位置关系是AF⊥BE; (2)成立,证明△ADE≌△DCF,然后证明△ABE≌△ADF即可证得BE=AF,然后根据三角形内角和定理证明∠AMB=90°,从而结论得证.
试题解析:
(1)AF=BE,AF⊥BE. 证明参考(2)
(2)结论成立.
证明:∵四边形ABCD是正方形,
∴BA=AD =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中, 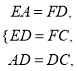
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,即∠BAE=∠ADF.
在△BAE和△ADF中, 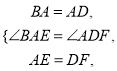
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)按照以上变换,那么f(g(a,b))等于( )
A. (﹣b,﹣a) B. (a,b) C. (b,a) D. (﹣a,﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年![]() 月的商品销售总额一共是
月的商品销售总额一共是![]() 万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
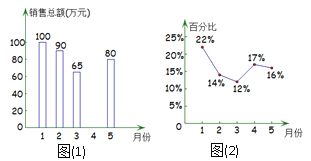
A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知x=﹣3是关于x的方程2k﹣x﹣k(x+4)=5的解,求k的值;
(2)在(1)的条件下,已知线段AB=12cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com