
【题目】为庆祝中华人民共和国成立70周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角为32°,测得“平安中心”AB的顶部A处的仰角为44°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,求平安金融中心AB的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,tan44°≈0.99,![]() 1.41,
1.41,![]() )
)

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
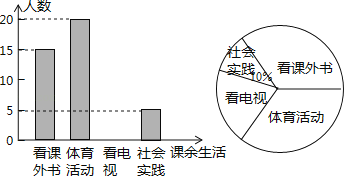
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P, AC=PC,∠COB=2∠PCB.
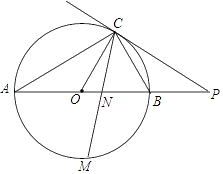
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山![]() 位于树的西面.山高
位于树的西面.山高![]() 为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢
为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢![]() 恰好与山峰
恰好与山峰![]() 处在同一条直线上,人眼离地7尺.则山高
处在同一条直线上,人眼离地7尺.则山高![]() 的长为(结果保留到整数,1丈=10尺)( )
的长为(结果保留到整数,1丈=10尺)( )
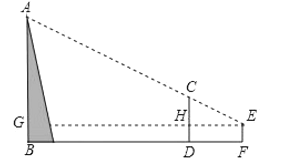
A.162丈B.163丈C.164丈D.165丈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明沿AB方向匀速前进的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
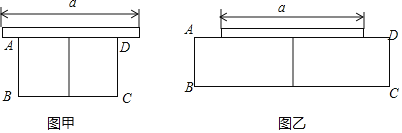
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com