
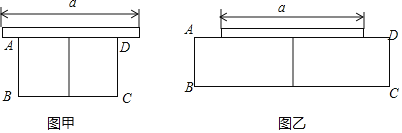
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.
【答案】(1)①AD的长是5米;②按图乙的方案,能围成的矩形花圃的最大面积是![]() 平方米;(2)第二种方案能围成面积最大的矩形花圃.
平方米;(2)第二种方案能围成面积最大的矩形花圃.
【解析】
(1)①设AB的长是x米,根据矩形的面积公式列出方程;
②列出面积关于x的函数关系式,再根据函数的性质解答;
(2)设AB=x,能围成的矩形花圃的面积为S,根据题意列出S关于x的函数关系,再通过求最值方法解答.
解:(1)①设AB的长是x米,则AD=20-3x,
根据题意得,x(20-3x)=25,
解得:x1=5,x2=![]() ,
,
当x=![]() 时,AD=15>6,
时,AD=15>6,
∴x=5,
∴AD=5,
答:AD的长是5米;
②设AB的长是x米,矩形花圃的最大面积是y平分米,则AD=![]() (20-3x+6),
(20-3x+6),
根据题意得,y=![]() x(20-3x+6)=-
x(20-3x+6)=-![]() x2+13x=-
x2+13x=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
答:按图乙的方案,能围成的矩形花圃的最大面积是![]() 平方米;
平方米;
(2)按图甲的方案,设AB=x,能围成的矩形花圃的面积为S,
∴S=x(20-3x)=-3x2+20x=-3(x-![]() )2+
)2+![]() ,
,
当x=![]() 时,AD=10>a,
时,AD=10>a,
故第二种方案能围成面积最大的矩形花圃.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
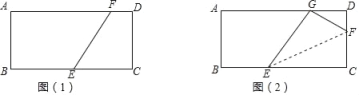
【题目】在矩形ABCD中,AB=4,AD=8.
(1)如图①若E从B到C运动,F从D到A运动且BE=2DF,
( i)当DF为何值时四边形ECDF是矩形.
( ii)当DF为何值时EF=2![]() .
.
(2)如图②E在BC上,BE=3,F在CD上,将△ECF沿EF折叠,当C点恰好落在AD边上的G处时,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.
(1)求证:CQ=QP
(2)设点Q的坐标为(x,y),求y关于x的函数关系式及自变量x的取值范围;
(3)如图2,连结OQ,OB,当点P在线段OA上运动时,设三角形OBQ的面积为S,当x取何值时,S取得最小值,并求出最小值;
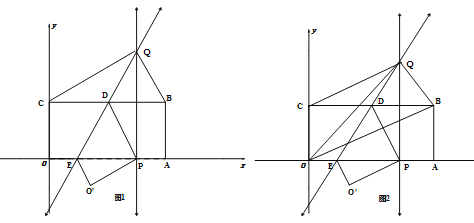
查看答案和解析>>
科目:初中数学 来源: 题型:
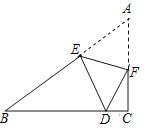
【题目】如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E、F分别在边AB、AC上,将△AEF沿直线EF折叠,使点A的对应点D恰好落在边BC上.若△BDE是直角三角形,则CF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
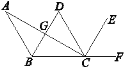
【题目】如图,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
(1)判断BD和CE的位置关系,并说明理由;
(2)判断AC和BD是否垂直,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
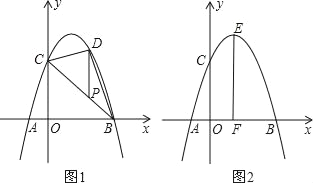
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
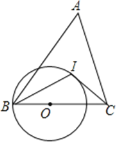
【题目】如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
(1)求证:CI是⊙O的切线;
(2)若AC=BC=5,AB=6,求BI的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com