
����Ŀ����ͼ��ʾ,������OABC����ƽ��ֱ������ϵ��,��A,C�ֱ���x,y�����������,��֪��B(4,2),������OABC����,ʹ�õ�C�Ķ�Ӧ��Pǡ�������߶�OA(�����˵�O,A)��,�ۺ�����ֱ�߷ֱ�BC��OA�ڵ�D��E������P���߶�OA���˶�ʱ,����P��OA�Ĵ��߽��ۺ�����ֱ���ڵ�Q.
��1����֤��CQ=QP
��2�����Q������Ϊ(x,y),��y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ;
��3����ͼ2,����OQ,OB,����P���߶�OA���˶�ʱ,��������OBQ�����ΪS,��xȡ��ֵʱ,Sȡ����Сֵ,�������Сֵ��
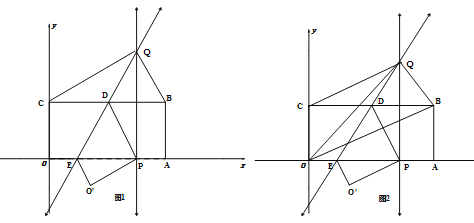
���𰸡���1��CQ=PQ��2��![]() ��3��
��3��![]()
�������������������1����CD=PD,��CDE=��PDE�õ���CDQ=��PDQ���ټ���DQ=DQ�ɵá�CDQ�ա�PDQ�����Ե�CQ=PQ����2����Q(x,y) ����CQ=PQ=y����QP��BC��H,��QH=y-2,CH=x���ɹ��ɶ�������![]() ������
������![]() ����3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)����
����3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)����![]() ������
������![]() ������
������![]() ������x=1ʱ��S����СֵΪ
������x=1ʱ��S����СֵΪ![]() ��
��
���������
��1������֪��CD=PD,��CDE=��PDE
�� ��CDQ=��PDQ
�֡�DQ=DQ
���CDQ�ա�PDQ
��CQ=PQ
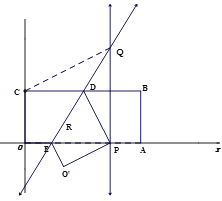
��2����Q(x,y)
CQ=PQ=y
��QP��BC��H,��QH=y-2,CH=x���ɹ��ɶ�������


��3����ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y)������![]()
![]() .
.
![]()
![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��m��1��2m���ĺ������������껥Ϊ�෴�������Pһ���ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
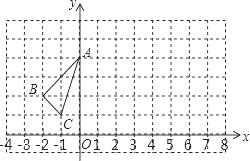
����Ŀ���ڱ߳�Ϊ1��С�����������У���ABC�Ķ�����ڸ���ϣ�
��1��B�����y��ĶԳƵ�����Ϊ ��
��2������ABC����ƽ��3����λ���ȵõ���A1B1C1���뻭����A1B1C1��
��3���ڣ�2���������£�A1������Ϊ ��
��4������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC���������λ����ͼ��ÿ��С�����εı߳���Ϊ1����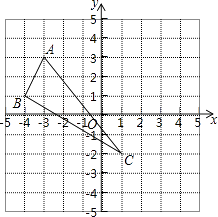
��1���뻭����ABC��x������ƽ��3����λ���ȣ�����y������ƽ��2����λ���Ⱥ�ġ�A��B��C�䣨����A�䡢B�䡢C��ֱ���A��B��C�Ķ�Ӧ�㣬��д��������
��2��ֱ��д��A�䡢B�䡢C����������꣺
A�䣨 �� ���� B�䣨 �� ����
C�䣨 �� ����
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ҹ���Լ��1.3�ڸ�Ѫѹ�����ߣ�ռ15���������˿�����10%��15%��Ԥ����Ѫѹ���ݺ��ӡ���ǧ��kpa���͡�������mmHg�����DZ�ʾѪѹ�ĵ�λ��ǰ���Ƿ����Ĺ��ʼ�����λ�����������ǹ�ȥһֱ�㷺ʹ�õĹ��õ�λ����������±����ṩ����Ϣ���ж����и��黻������ȷ���ǣ� ��
ǧ��kpa | 10 | 12 | 16 | �� |
������mmHg | 75 | 90 | 120 | �� |
A. 18kpa=135mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 32kpa=240mmHg
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��DE����ABC��70����CDE��140�����BCD��ֵΪ( )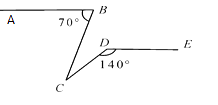
A.70
B.50
C.40
D.30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD��ֱ��MN�ֱ�AB��CD��M��N���㣬��ME��NF�ֱ��ǡ�AMN����DNM�Ľ�ƽ���ߣ���˵����ME��NF
�⣺��AB��CD��(��֪)
���AMN����DNM()
��ME��NF�ֱ��ǡ�AMN����DNM�Ľ�ƽ���ߣ�(��֪)
���EMN����AMN��
��FNM����DNM (��ƽ���ߵĶ���)
���EMN����FNM(��������)
��ME��NF()
�ɴ����ǿ��Եó�һ�����ۣ�
����ƽ���߱�������ֱ�����أ�һ���ǵ�ƽ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�죬С����ֽ��д��һ����ʽ��4x2��8x��11������С��˵��������xȡ��ֵ���������ʽ��ֵ������ֵ����������һ�ԣ���С�ն�����������Σ��������С����˵��С�պ���������������ѧ��֪ʶ˵��һ�����еĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD�ı�AD��x���ϣ���A��ԭ�㣬AB=3��AD=6����������ÿ��2����λ������x���������������˶���ͬʱ��P��A�������ÿ��1����λ������A��B��C��D��·���������˶�����P���˶���D��ʱֹͣ�˶�������ABCDҲ��ֹ֮ͣ�˶���
��1����P���A���˶���D�������ʱ�䣻
��2����P����˶�ʱ��Ϊt���룩��
�ٵ�t=8ʱ�������P�����ꣻ
������OAP���ΪS����̽����P���˶�������S��t֮��Ĺ�ϵʽ��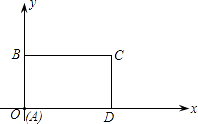
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com